Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Thévenin e Norton

Ver Teoria
Exercício 51234678910

Enunciado

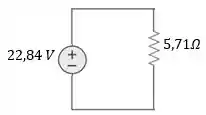
Use transformação de fontes para reduzir o circuito da figura a uma única fonte de tensão em série com um único resistor.

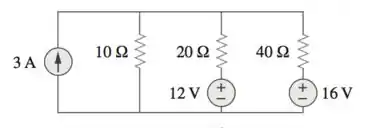
Passo 1

Utilizando a transformação de fontes, vamos transformar as fontes de tensão em série com os resistores em fontes de corrente em paralelo com os resistores.

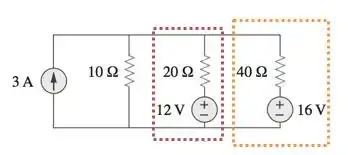
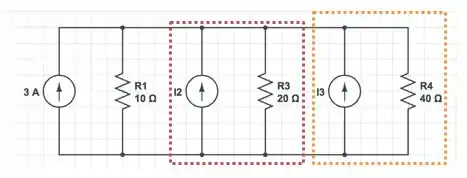
Passo 2

Próximo passo é calcular os valores de I 2 e I 3 .

I 2 = 12 20 = 0,6 A

I 3 = 16 40 = 0,4 A

Passo 3

Como as três fontes de corrente estão em paralelo e no mesmo sentido, para obter a corrente total do circuito temos que somar a contribuição de cada fonte de corrente:

I T = I 1 + I 2 + I 3

I T = 3 + 0,6 + 0,4

I T = 4   A

Passo 4

Agora temos que calcular a resistência equivalente do circuito. Como todas as resistências estão em paralelo:

R e q = 1 1 10 + 1 20 + 1 40

R e q = 5,71 Ω

Passo 5

Até agora o nosso circuito está assim:

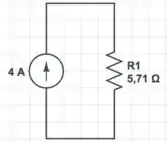
Como foi pedido um circuito equivalente com uma fonte de tensão em série com um resistor, a gente precisa fazer a transformação para o circuito com a fonte de tensão:

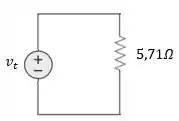
Logo:

v t = 5,71 * 4 = 22,84 V

Portanto:

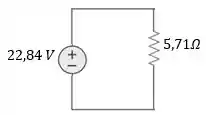
Resposta

Exercícios de Livros Relacionados

47- Obtenha os circuitos equivalentes de Thévenin e de Norton do circuito na Figura 4.114 em relação aos terminais a - b .
36- Calcule a corrente i no circuito da Figura 4.103 usando o teorema de Thévenin. (Sugestão: Determine o equivalente de Thévenin visto pelo resistor de 12Ω .)
Obtenha o equivalente de Norton em relação aos terminais a, b do circuito da Figura P4.81.
23- Consultando a Figura 4.91 , use transformação de fontes para determinar a corrente e a potência no resistor de 8Ω .
25- Determine v o no circuito da Figura 4.93 usando transformações de fontes. Verifique seu resultado usando o P S p i c e ou M u l t i S i m