Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Thévenin e Norton

Ver Teoria
Exercício 71234568910

Enunciado

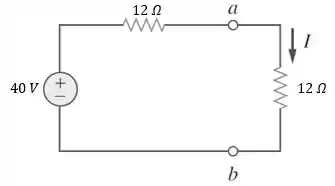
Para o circuito da figura abaixo:

  1. Obtenha o equivalente de Thévenin para os terminais a - b .
  2. Calcule a corrente quando R L = 8   Ω .
  3. Calcule R L para que a potência transferida para ele seja a máxima.
  4. Determine a potência máxima.

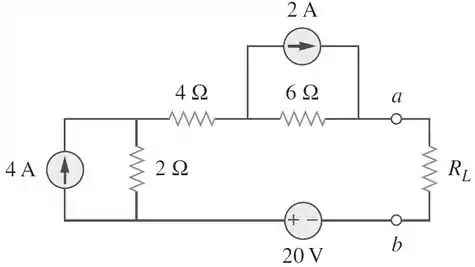
Passo 1

Na letra (a), precisamos encontrar o circuito equivalente de Thévenin para o circuito à esquerda dos terminais a - b , como no esquema abaixo:

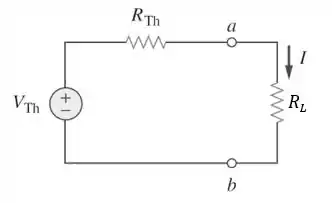
Passo 2

Primeiro, vamos determinar R T h . Para isso, vamos desligar todas as fontes independentes e calcular a resistência equivalente vista pelos terminais a - b :

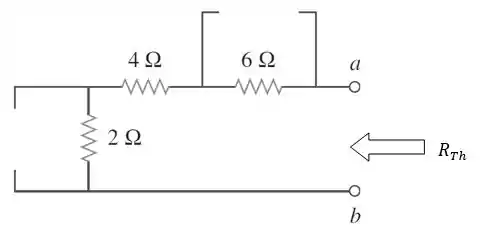
Ajeitando melhor o circuito, veremos que os resistores passaram a ficar associados em série:

R T h = 6 + 4 + 2

R T h = 12   Ω

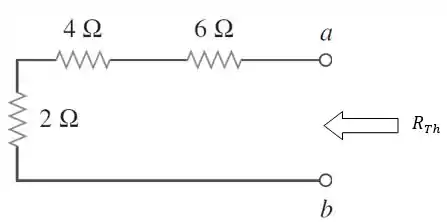
Passo 3

Agora, precisamos encontrar V T h que é a tensão de circuito aberto nos terminais a - b :

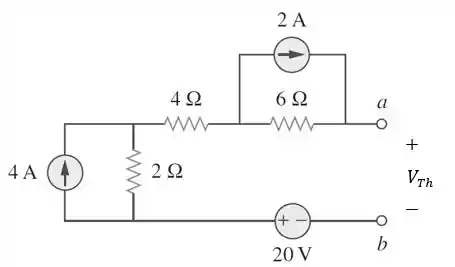
Passo 4

Encontraremos o valor de V T h utilizando o princípio da superposição. Primeiro consideraremos a fonte de tensão de 20   V . Desse modo, desligaremos as duas fontes de corrente, ou seja, vamos substituí-las por um circuito aberto:

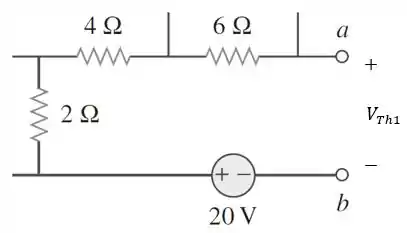
Como o circuito está aberto, não há circulação de corrente. Logo, não possui queda de tensão nos resistores e V T h 1 será o próprio valor da fonte de tensão.

V T h 1 = 20   V

Passo 5

Agora, vamos considerar apenas a fonte de corrente de 4   A , ou seja, desligaremos a fonte de tensão e a fonte de corrente de 2   A .

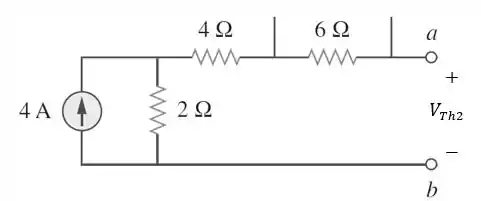
Como os terminais a - b estão abertos, toda a corrente fornecida pela fonte de corrente de 4   A fica circulando pela malha fechada, como na figura abaixo:

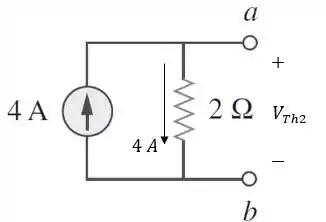
Logo, pela lei de Ohm:

V T h 2 = 2 × 4 = 8   V

Passo 6

Agora, vamos considerar apenas a fonte de corrente de 2   A , ou seja, desligaremos a fonte de tensão e a fonte de corrente de 4   A .

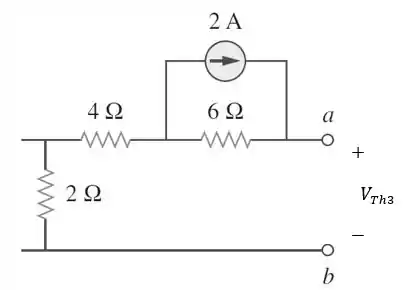
Pelo mesmo motivo do passo anterior, a corrente fornecida pela fonte de corrente de 2   A fica circulando pela malha fechada, como na figura abaixo:

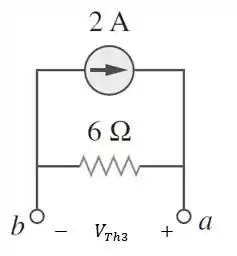
Logo, pela lei de Ohm:

V T h 3 = 6 × 2 = 12   V

Passo 7

Logo, pelo princípio da superposição, V T h será a soma das contribuições das três fontes:

V T h = V T h 1 + V T h 2 + V T h 3

Substituindo:

V T h = 20 + 8 + 12 = 40   V

Passo 8

Logo, o circuito equivalente de Thévenin à esquerda dos terminais a - b , será:

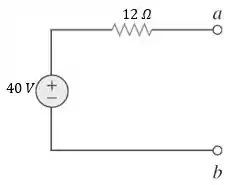
Passo 9

Na letra (b), precisamos encontrar I quando R L = 8   Ω . Para isso, vamos conectar o resistor de 8   Ω à direita dos terminai a - b :

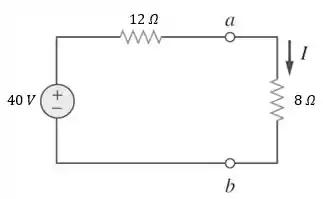
Aplicando a lei de Ohm:

I = 40 ( 12 + 8 ) = 2   A

Passo 10

A máxima transferência de potência ocorre quando a resistência de Thévenin é igual à resistência conectada aos terminais a - b , ou seja:

R T h = R L

Logo,

R L = 12   Ω

Passo 11

Para terminar, precisamos calcular a potência máxima, ou seja, a potência para quando R T h = R L :

Pela definição de potência:

P = R L × I 2

Substituindo:

P = 12 × 40 12 + 12 2

P = 33,33   W

Resposta

L e t r a   a :   V T h = 4 0   V ;   R T h = 12   Ω

L e t r a   b :   I = 2   A

L e t r a   c : R L = 12   Ω

L e t r a   d : P = 33,33   W

Exercícios de Livros Relacionados

47- Obtenha os circuitos equivalentes de Thévenin e de Norton do circuito na Figura 4.114 em relação aos terminais a - b .
36- Calcule a corrente i no circuito da Figura 4.103 usando o teorema de Thévenin. (Sugestão: Determine o equivalente de Thévenin visto pelo resistor de 12Ω .)
Obtenha o equivalente de Norton em relação aos terminais a, b do circuito da Figura P4.81.
23- Consultando a Figura 4.91 , use transformação de fontes para determinar a corrente e a potência no resistor de 8Ω .
25- Determine v o no circuito da Figura 4.93 usando transformações de fontes. Verifique seu resultado usando o P S p i c e ou M u l t i S i m