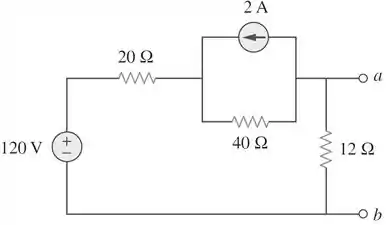
Determinar o equivalente de Norton em relação aos terminais no circuito mostrado na figura:
Passo 1
O circuito equivalente de Norton é igual ao da figura abaixo:
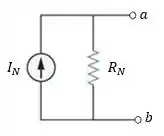
Então, precisaremos calcular e .
Passo 2
Primeiro calcularemos o . Como ele é calculado da mesma forma que o , vamos curto-circuitar a fonte de tensão e substituir a fonte de corrente por um circuito aberto:
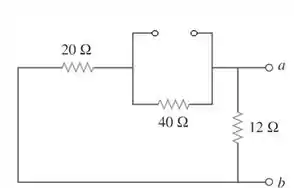
Agora, ajeitando o circuito, ele fica assim:
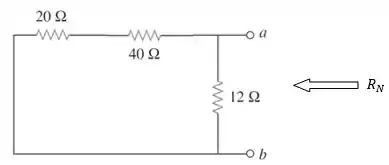
Lembrando que é a resistência vista pelos terminais Portanto:
Passo 3
Agora precisaremos calcular , que é a corrente que passa nos terminais quando este é curto-circuitado:
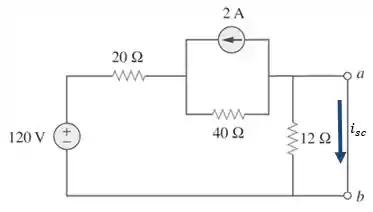
Passo 4
Podemos utilizar a transformação de fontes para facilitar o cálculo da corrente :
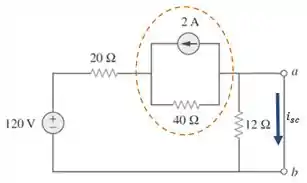
![]()
De acordo com a transformação de fontes do circuito acima:
Passo 5
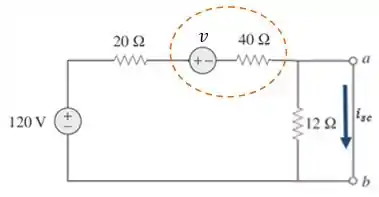
É importante lembrar que quando curto-circuitamos os terminais a corrente passará toda pelo curto-circuito, que é um “caminho mais fácil” do que aquele com o resistor de . Agora temos o circuito abaixo e finalmente podemos calcular a :
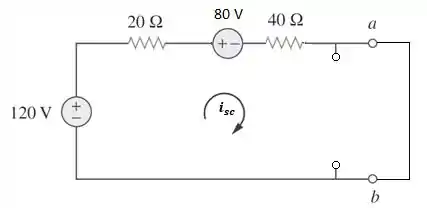
Aplicando a LTK ao circuito acima:
Logo, como a corrente de Norton é igual à de curto-circuito:
Passo 6
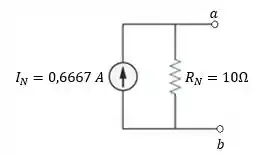
Resposta