Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Thévenin e Norton

Ver Teoria
Exercício 31245678910

Enunciado

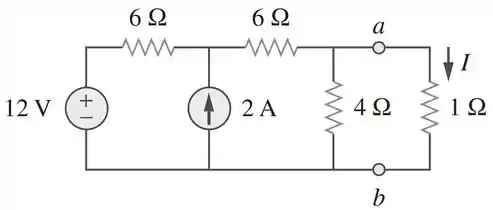
Usando o teorema de Thévenin, determine o circuito equivalente à esquerda dos terminais do circuito abaixo. Em seguida, determine I .

Passo 1

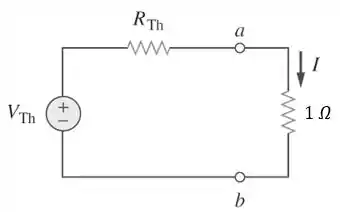
Precisamos encontrar o circuito equivalente de Thévenin para o circuito à esquerda dos terminais a - b , como no esquema abaixo:

Passo 2

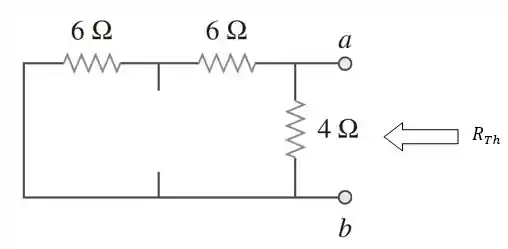
Primeiro, vamos determinar R T h . Para isso, vamos desligar todas as fontes independentes e calcular a resistência equivalente vista pelos terminais a - b :

O resistor de 4 Ω está em paralelo com a associação em série dos dois resistores de 6 Ω:

R T h = ( 6 + 6 ) 4

R T h = 12 × 4 12 + 4 = 48 16

R T h = 3   Ω

Passo 3

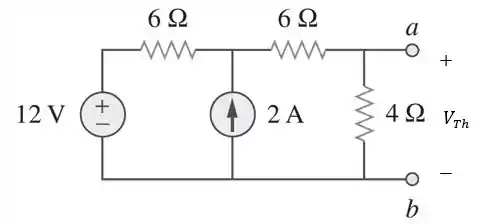
Agora, precisamos encontrar V T h que é a tensão de circuito aberto nos terminais a - b :

Passo 4

Encontraremos o valor de V T h utilizando o princípio da superposição. Primeiro consideraremos a fonte de tensão de 12   V . Desse modo, desligaremos a fonte de corrente, ou seja, vamos substituí-la por um circuito aberto:

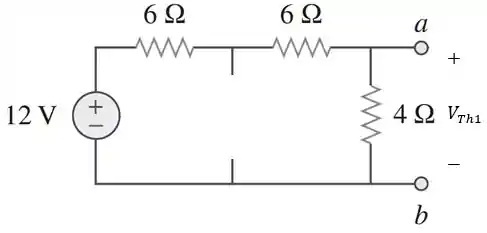
Agora, vamos aplicar divisor de tensão para encontrar V T h 1 :

V T h 1 = 4 6 + 6 + 4 × 12

V T h 1 = 3   V

Passo 5

Agora, vamos considerar apenas a fonte de corrente, ou seja, desligaremos a fonte de tensão. Então, vamos substituí-la por um curto-circuito:

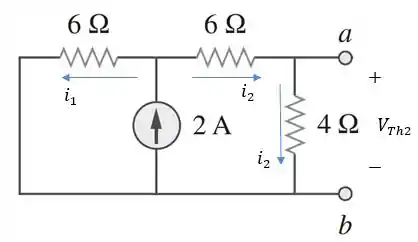
Utilizando divisor de corrente:

i 2 = 6 6 + 6 + 4 × 2

i 2 = 0,75   A

Logo, pela lei de Ohm:

V T h 2 = 4 × 0,75 = 3   V

Passo 6

Logo, pelo princípio da superposição, V T h será a soma das contribuições das duas fontes:

V T h = V T h 1 + V T h 2

Substituindo:

V T h = 3 + 3 = 6   V

Passo 7

Logo, o circuito equivalente à esquerda dos terminais a - b , será:

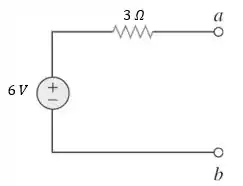
Passo 8

Para finalizar, precisamos encontrar I . Para isso, vamos conectar o resistor de 1   Ω à direita dos terminai a - b :

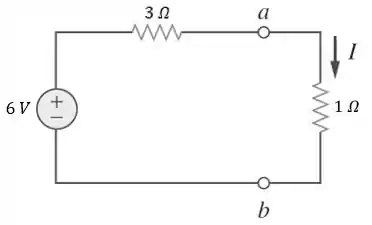
Aplicando a lei de Ohm:

I = 6 4 = 1,5   A

Resposta

V T h = 6   V

R T h = 3   Ω

I = 1,5   A

Exercícios de Livros Relacionados

47- Obtenha os circuitos equivalentes de Thévenin e de Norton do circuito na Figura 4.114 em relação aos terminais a - b .
36- Calcule a corrente i no circuito da Figura 4.103 usando o teorema de Thévenin. (Sugestão: Determine o equivalente de Thévenin visto pelo resistor de 12Ω .)
Obtenha o equivalente de Norton em relação aos terminais a, b do circuito da Figura P4.81.
23- Consultando a Figura 4.91 , use transformação de fontes para determinar a corrente e a potência no resistor de 8Ω .
25- Determine v o no circuito da Figura 4.93 usando transformações de fontes. Verifique seu resultado usando o P S p i c e ou M u l t i S i m