Determine no circuito da figura usando transformação de fontes.
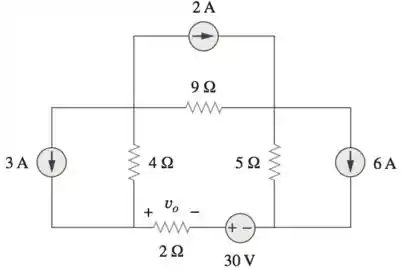
Passo 1
Se a gente analisar, dá pra transformar as fontes de corrente em paralelo com as resistências em fontes de tensão em série com as resistências e, então, o circuito ficará assim:
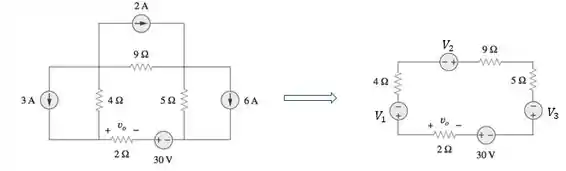
Lembrar que, após a transformação, o positivo da fonte de tensão fica no lugar da ponta da seta da fonte de corrente.
Passo 2
Agora precisamos calcular o valor de , e :
Passo 3
Agora aplicaremos a LTK na malha para calcularmos a corrente:
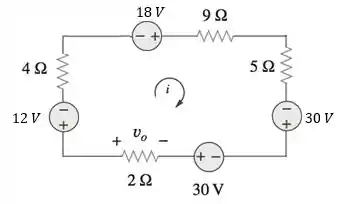
Aplicando o equacionamento de malha, com a LKT, na única malha que temos, portanto, a corrente que passar pelo resistor de , é a mesma que passa por todos os outros elementos do circuito.
Passo 4
Agora já temos tudo para calcular o . Só repare no seguinte: pela imagem anterior, podemos ver que, pelo sentido da corrente e pelos sinais da tensão , o resistor está no sentido oposto do que deveria estar.
Isso porque devemos ter uma queda de tensão ao passar por um resistor, mas pela tensão , vemos que a corrente está indo do para o . Logo, está no sentido contrário e, por isso, vamos colocar um sinal negativo no cálculo dele, beleza?
De acordo com a Lei de Ohm: