Um fabricante de latas para conservas sabe que deve ajustar o equipamento que produz as latas se o valor médio do peso for maior ou igual ao peso relatado na lata, e que é de gramas. Para decidir sobre o que fazer, o fabricante obteve uma amostra de latas retiradas ao acaso do estoque produzido, pesou as latas e obteve um peso médio igual a gramas e um desvio padrão amostral igual a gramas. Sabe-se ainda, da história do processo e de testes efetuados, que o verdadeiro desvio padrão é de gramas.

Pede-se:

1. Especifique as hipóteses para conduzir um teste para a média com o intuito de encontrar a decisão que o fabricante deve tomar.

1. Qual é a formulação e a decisão do teste de hipótese aos níveis de significância e admitindo que o desvio padrão é desconhecido?

Mostre os resultados através do cálculo da estatística do teste. Esboce um gráfico da distribuição do teste indicando claramente a área de rejeição e aceitação de .

b)

Como , vamos usar a distribuição T-Student para tomar nossas decisões.

Vamos calcular primeiramente nossa estatística de teste para teste de hipótese da média:

Lembrando que aqui estamos considerando o desvio padrão desconhecido, então usamos o desvio padrão amostral que é igual a gramas. Como (pois temos latas na amostra), (sempre é o valor que usamos para construir nossas hipóteses), e a média amostral encontrada foi , nosso fica:

Nosso ponto crítico no teste unilateral inferior é dado por:

Primeiramente, vamos testar para :

E como vamos ter graus de liberdade. Procurando esse cara na tabela T de Student:

Então nossa estatística de teste fica fora da região crítica:

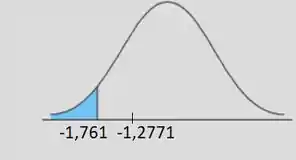
E isso significa que não rejeitamos a hipótese nula!

Agora vamos testar para para . Nosso ponto crítico vai ser:

Para grau de liberdade :

Então nossa estatística de teste também fica fora da região crítica:

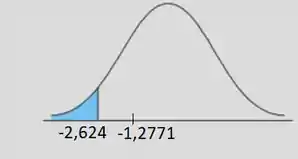
Então nós não rejeitamos nossa hipótese nula!