Cada uma das conexões uniformes do conjunto tem massa e comprimento A posição de equilíbrio do conjunto, no plano vertical, é determinada pelo binário , aplicado à conexão da esquerda. Expresse em função de
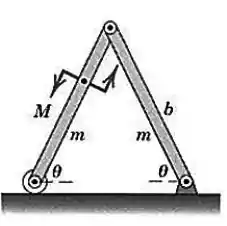
Passo 1
Para achar o ângulo de equilíbrio, vamos ter que primeiro calcular o trabalho virtual de cada força e depois usar o princípio do trabalho virtual:
Passo 2
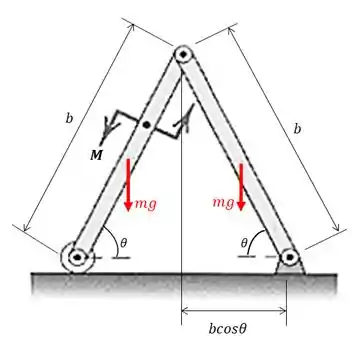
Perceba que a distância do ponto de aplicação da força peso, de ambas as barras, até o chão vale .
O trabalho virtual valerá:
E é negativo já que exibe uma tendência a diminuir a distância .
Mas como são duas barras, temos duas forças peso:
Passo 3
Já o trabalho virtual do momento pode ser escrito por:
Positivo já que o momento, por estar girando no sentido anti-horário que é o sentido natural de crescimento dos ângulos, tende a aumentar o ângulo. Assim:
Uma vez que , temos então: