A mola de constante não está distendida quando . Obtenha uma expressão para a força necessária para defletir o sistema de um ângulo A massa das barras é desprezível.
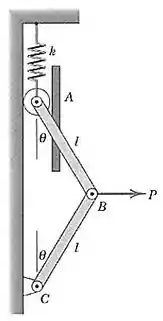
Passo 1
Vamos usar o princípio dos trabalhos virtuais:
Neste caso, temos duas forças: a força da mola () e a força
Podemos esquematizar isso assim:
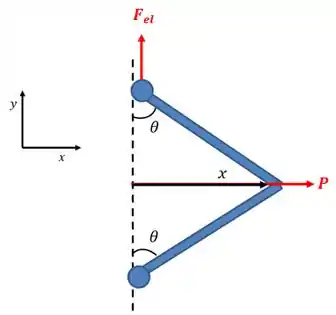
Repare que a força elástica está na direção , então vamos ter que o trabalho virtual da força elástica é:
Considerando:
A força elástica está fazendo com que y diminua, por isso seu trabalho é negativo.
Já a força está na direção , e fazendo com que aumente, então o trabalho da força é:
Passo 2
Beleza, agora precisamos melhorar a descrição do nosso sistema. A força elástica é dada por:
Quanto vale
Bom, pense no seguinte: se não houvesse , a barra ficaria totalmente esticada:
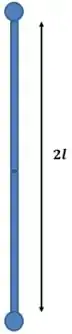
Com a força , o sistema fica assim:
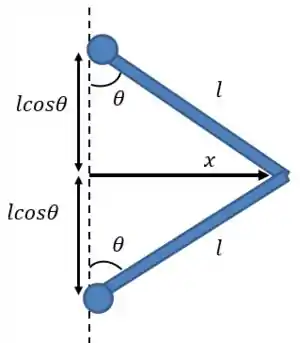
Como a mola está conectada na parte circular superior, ela teve que se deslocar, certo?
Esse deslocamento será o comprimento máximo que a barra pode ter quando está esticada que é de menos o comprimento inicial que é :
Sendo assim, a força elástica será dada por:
Passo 3
Mas para achar o trabalho virtual da força elástica temos que derivar a equação de em função de :
Assim:
Passo 4
E o trabalho da força
Quanto vale Bem, basta olhar os triângulos desenhados antes.
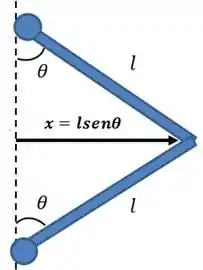
Então, a derivada de em função de é:
Assim:
Passo 5
Agora vamos ter que a soma dos trabalhos virtuais deve ser nula:
Vamos cortar e arrumar isso aí: