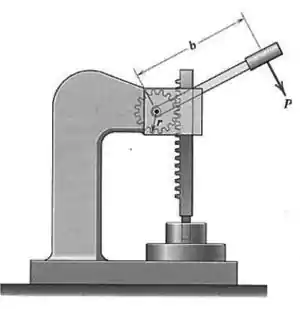
A prensa trabalha por meio de um mecanismo de cremalheira e pinhão, e é usada para gerar grandes forças, tais como as necessárias para produzir encaixes por pressão. Se o raio médio das engrenagens do pinhão vale , determine a força que pode ser gerada pela prensa para uma dada força na manopla.
Passo 1
Temos que saber que o trabalho virtual total de todas as forças tem que ser nulo:
Então, vamos calcular o trabalho virtual de cada uma das forças e depois somá-los.
Passo 2
Se a manopla exerce uma força na superfície, a superfície exercer uma força na manopla, não é mesmo?
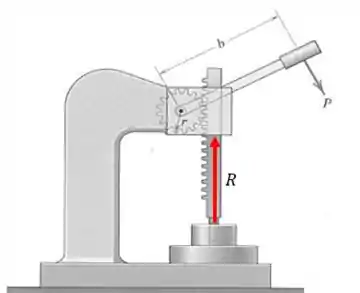
Na própria figura podemos ver que a força se encontra a uma distância do centro da engrenagem, então o seu trabalho virtual será:
E a força se encontra a uma distância do centro da engrenagem, logo seu trabalho virtual é:
Repare que eles têm sinais contrários, pois produzem momentos contrários!!!
Passo 3
Agora vamos somar esses dois momentos:
Assim: