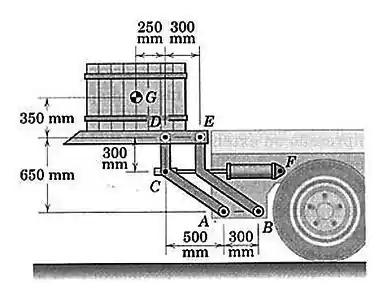
Uma plataforma automática de carga, projetada para a traseira de um caminhão, está mostrada na figura. A posição da plataforma é controlada pelo cilindro hidráulico, que aplica força em . As conexões são articuladas à estrutura do caminhão em , e . Determine a força fornecida pelo cilindro para sustentar a plataforma na posição mostrada. A massa da plataforma e das conexões pode ser desprezada em comparação com a massa do caixote de com centro de massa em .
Passo 1
Vamos usar o princípio dos trabalhos virtuais:
Neste caso, temos duas forças: a força fornecida pelo cilindro e a força peso do caixote .
Podemos esquematizar isso assim:
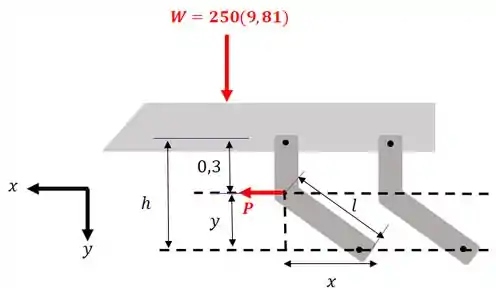
Repare que a força peso está no sentido positivo do eixo , então vamos ter que o trabalho virtual desta força é:
Já a força está no sentido positivo do eixo , então o trabalho da força é:
Passo 2
Beleza, agora precisamos melhorar a descrição do nosso sistema. A força peso é dada por:
Vamos analisar a geometria do nosso problema!
Pense no seguinte: a força garante que a plataforma fique exatamente na posição da figura. Então, vamos analisar este triângulo retângulo aqui:
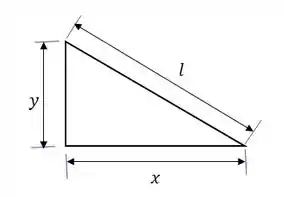
Temos que:
Se derivarmos isso, vamos ter que:
Passo 3
Então, o trabalho virtual da força peso vai ser:
Passo 4
Agora vamos ter que a soma dos trabalhos virtuais deve ser nula:
Vamos cortar e arrumar isso aí:
Agora é só substituirmos os valores de e conforme foi indicado na figura do enunciado:
Então: