Determine, em função do ângulo , o momento , aplicado através do eixo à conexão inferior, necessário para suportar a carga . Despreze os pesos das partes.
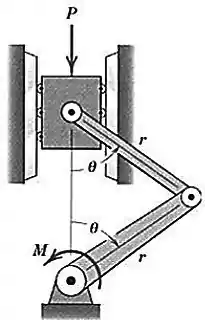
Passo 1
Temos duas coisas que exercem trabalho no sistema: A força e o momento
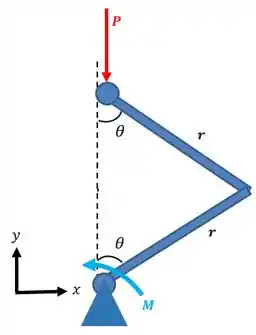
A força tem uma tendência a diminuir o comprimento , então seu trabalho é negativo:
E o momento tem uma tendência a diminuir o ângulo, então seu trabalho também é negativo:
Passo 2
Perceba que o comprimento é:
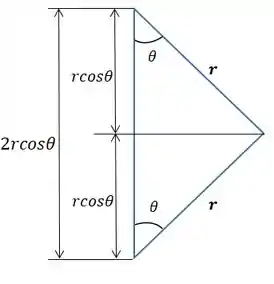
Precisamos derivar isso aí em função de :
Assim, o trabalho da força é:
Passo 3
Agora vamos usar o Princípio do Trabalho Virtual que diz que o somatório do trabalho virtual de cada força deve ser zero:
Como queremos saber o momento , teremos que: