O cilindro hidráulico é usado para afastar as conexões e elevar a carga Determine a força compressiva no cilindro, para a posição mostrada. Despreze a massa de todas as partes, à exceção de
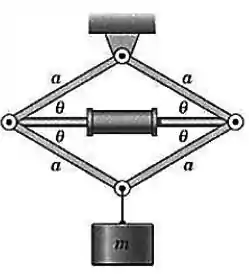
Passo 1
Repare que a estrutura formada pelas barrinhas comprime o cilindro, então o cilindro faz a seguinte força na estrutura:
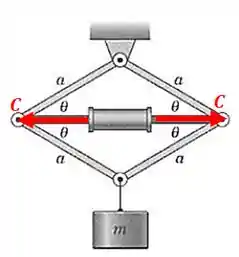
Mas isso tudo é causado pela a ação do peso:
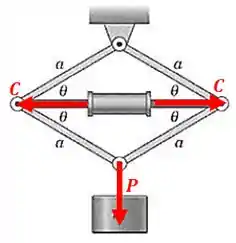
Passo 2
Vamos primeiro calcular o trabalho das forças
O comprimento que cada uma distende é dado por:
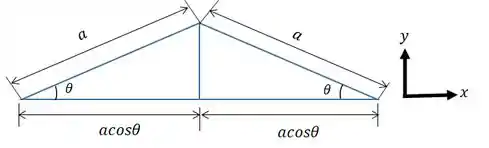
Como temos duas forças, vamos ter que:
Agora temos que derivar o comprimento em função de :
Então, vamos ter que:
Passo 3
Já o comprimento que o peso estica é dado por:
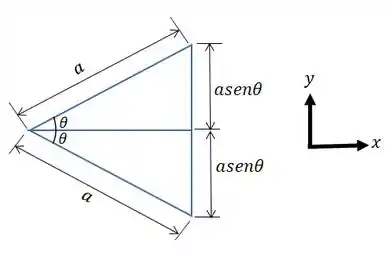
Pera, mas pela figura dá pra ver que ele vai esticar o negócio em cima e embaixo, assim:
Então, o trabalho da força peso é:
Agora precisamos derivar a comprimento em função de :
Então, temos que:
Passo 4
Sabemos que a soma do trabalho virtual de cada força deve ser zero:
Como queremos saber a força compressiva: