Por meio de um mecanismo de cremalheira e pinhão, grandes forças podem ser desenvolvidas pelo saca-rolhas mostrado. Se o raio médio das engrenagens do pinhão vale 12 mm, determine a força que é exercida sobre a rolha para as forças dadas, , nas manoplas.
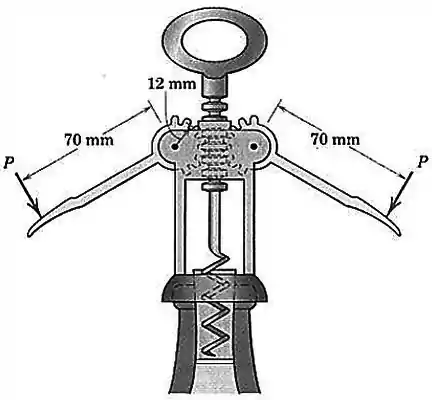
Passo 1
O nosso sistema acima pode ser representado assim:
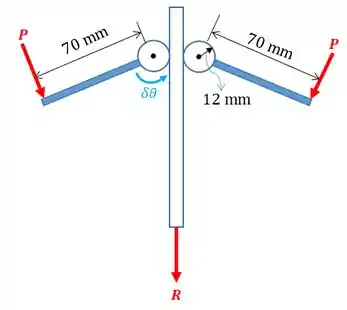
Passo 2
Perceba que a força está afastada do centro da engrenagem, então o seu trabalho é:
Já a força está afastada do centro da engrenagem, então o seu trabalho virtual é:
Mas repare que a força faz a engrenagem girar no sentido contrário ao movimento provocado pela força , então seu trabalho será negativo:
Esse aparece porque estamos lidando com um movimento de rotação da engrenagem!!!
Passo 3
Agora vamos aplicar o princípio dos trabalhos virtuais que diz que o somatório do trabalho que cada força produz deve ser zero:
Não esqueça que temos duas forças , então:
Como queremos determinar , vamos ter que: