Determine as componentes do vetor de ponto inicial e ponto final
Passo 1
Faaaala galerinhaa !! Prontos para começar mais uma questão?!
Beleza, nossa questão pede pra gente achar as componentes do vetor que vai do ponto ao ponto . Então vamos primeiro entender o que é um vetor.
Bom, os vetores são aqueles segmentos de reta que possuem um certo “tamanho” e “apontam” para um certo ponto, ou seja, possuem direção e sentido !!
Aqui na álgebra os vetores deve sair da origem e chegar até o ponto de interesse, certo? Mas nem sempre isso acontece !!
Muitas vezes, como aqui, o vetor sai de um ponto e vai para . Como na figura:
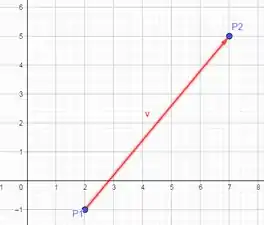
Para achar o vetor vamos começar traçando um vetor que vamos chamar de , que vai da origem até , e outro que chamaremos de , que vai da origem até :
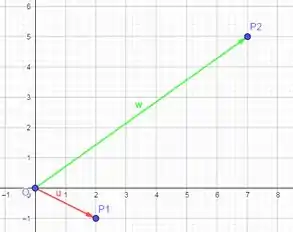
E agora? Como faremos para achar o vetor propriamente dito?
Pra isso, basta fazermos uma subtração de vetores. Como queremos que saia de e chegue em , temos que fazer o vetor final menos o vetor inicial:
A ordem certa é muito importante, pois é ela quem vai indicar o sentido do nosso vetor. Se trocarmos a ordem dos vetores na subtração, o vetor resultante vai ficar apontando no sentido contrário e ficará errado. Então, bastante atenção na ordem, ok!
Passo 2
Então galerinha, pra fazer essa subtração vamos lembrar que os vetores podem ser escritos como matriz coluna, ou seja:
Como nossos pontos e têm coordenadas e ! Então, temos vetores no espaço bidimensional,
Colocando na subtração:
Para fazer a subtração entre essas matrizes, temos que subtrair os elementos que estão na mesma posição das duas matrizes.
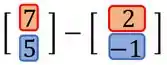
Subtraimos o primeiro termo de lá do primeiro termo de e assim por diante!
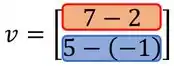
Encontramos as coordenadas do nosso vetor resultante:
Tranquilinho, não foi ?!
Bora seguir?