Se e , determine
Passo 1
Mais uma pra nossa seção, ein?!
O que o exercício está querendo é que a gente faça a soma entre esses dois vetores, então vamos lá!
Os vetores sempre podem ser escritos na forma matricial. Pra isso, nós construímos uma matriz coluna com cada linha correspondendo a uma coordenada do nosso vetor.
Então vamos fazer isso?
Agora vamos realizar a soma dessas matrizes que acabamos de encontra.
Colocando na soma:
Para somar duas matrizes, somamos os elementos que ocupam as mesmas posições. Ou seja, o primeiro elemento de uma coluna com o primeiro da outra, e assim sucessivamente:
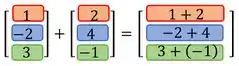
E assim encontramos a soma que estávamos procurando.