Encontre o produto escalar entre os vetores e , mostrados na Figura
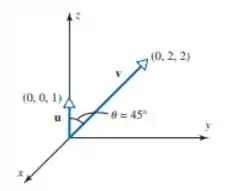
Passo 1
E para fechar com chave de ouro vamos fazer mais uma!!
O produto escalar entre dois vetores pode ser calculado como:
Mas, no nosso caso, temos o ângulo de 45° ali. Então o produto escalar pode ser calculado levando em consideração esse ângulo, através da expressão:
Veja que devemos fazer o módulo de um, vezes o módulo do outro, vezes o cosseno do ângulo entre eles.
Vamos começar lembrando a fórmula do módulo?
- Para
- Agora vamos fazer o módulo de
Substituindo:
Podemos simplificar a raiz de oito, lembrando que
Com isso, o que está dentro da raiz, pode sair da raiz, ficando:
E esse é o módulo de
Passo 2
Agora vamos colocar tudo que descobrimos na expressão do produto escalar.
Se o ângulo entre os vetores é
Aqui precisaremos substituir o cosseno de , que vale
Ficando com:
Note que temos multiplicando e dividindo, então vamos cortar, ficando só com:
E assim, encontramos nosso produto escalar!
Passo 3
Que tal fazer o teste com a outra fórmula só para ver no que dá?
Igualzinho, não é?
Então vocês podem usar as duas formas, cabe a você avaliar qual será melhor para cada situação!!
E assim nós chegamos ao fim de mais uma seção!!