Se , determine
Passo 1
Mais uma questão pra gente ficar craque em vetores e suas manipulações!!
Nela, o que nós teremos que fazer é determinar o triplo do vetor, já que ele pediu pra gente descobrir quem é .
Vamos começar desenhando este vetor?
Em álgebra podemos representar os vetores saindo da origem e indo até um certo ponto, que possui as mesmas coordenadas do vetor. No nosso caso nós chamamos este vetor de !
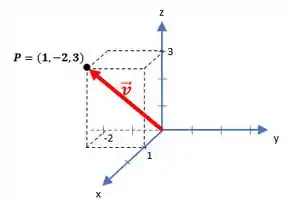
Então, como os vetores podem ser escritos como matriz coluna, nosso vetor se transforma em:
Onde o primeiro elemento indica a coordenada o , o segundo a coordenada e o terceiro a coordenada ! Então, temos um vetor no espaço tridimensional,
Pra encontrar o triplo deste vetor, vamos fazer a multiplicação dele por :
Como estamos multiplicando um número real por uma matriz, este vai multiplicar cada elemento da matriz coluna, como se fosse uma grande distributiva:
Resolvendo as multiplicações, teremos:
Vamos desenhar pra ver como agora este vetor está três vezes maior?
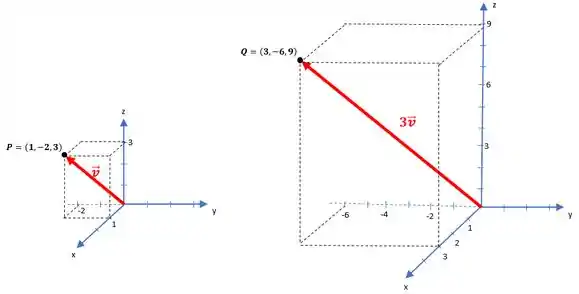
Muita diferença, não é? O que a gente pode perceber também é que na multiplicação por 3, só o que mudou foi o tamanho do vetor, mas ele continua com a mesma direção e o mesmo sentido!
E com isso encontramos nossa resposta.