Calcule as reações em para a viga submetida à carga distribuída triangular.
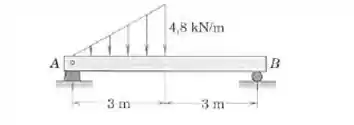
Passo 1
A primeira coisa que vemos entender nesse problema é que o carregamento triangular vai ser substituído por uma força concentrada de igual intensidade e aplicada no centroide do triângulo, vamos chamar essa força de .
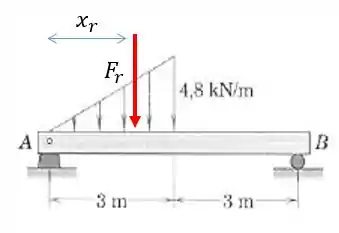
Temos que atender a duas condições de equilíbrio:
Sendo que em relação ao momento, vamos usar como referência o ponto , pois assim, vamos retirar duas incógnitas que desconhecemos e .
Passo 2
A força resultante devido à distribuição de forças contínua é dada pela área do triângulo:
E a posição em relação a
Vai ser dada por da base do triângulo:
Passo 3
Como estamos usando o ponto como referência, a força de reação não exercerá momento. Sendo assim:
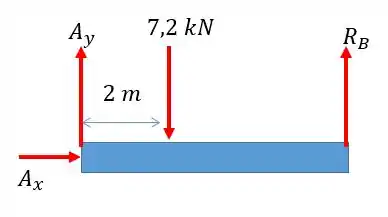
Considerando o sentido anti-horário positivo:
Passo 4
Agora é só usar a soma de forças: