Determine as reações em para a viga em balanço submetida às cargas concentrada e distribuída.
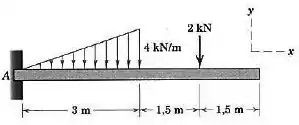
Passo 1
A viga precisa satisfazer a duas condições:
Passo 2
Vamos primeiro calcular a força de reação vertical. Pra isso, vamos escrever antes que:
Onde é a força concentrada que representa a distribuição linear de força. Essa força pode ser calculada pela área do triângulo, como já sabemos:
Assim:
Passo 3
Agora vamos para o momento. Existe um momento em , , que equilibra os momentos das forças, tanto a concentrada quanto a distribuída:
Perceba que a distância da força de até vale .
E onde está localizada a força concentrada que é resultante da distribuição de forças? No baricentro do triângulo! Assim:
Assim:
Assim:
Resposta
Exercícios de Livros Relacionados
Se a massa do contrapeso em A é 6500k g , determine a força que a comporta exerce sobre o anteparo liso em C . A comporta é articulada em B e tem 1m de largura. A densidade da água é ρ w = 1M g / m 3
Determine a massa do contrapeso A se a comporta de 1m de largura está prestes a abrir quando a àgua está no nível mostrado. A comporta é articulada em B e mantida pelo anteparo liso em C . A densidade
A placa de aço elíptica B é usada para selar a abertura no tanque de armazenamento de água. Determine a intensidade da força hidrostática resultante que atua sobre ela. A densidade da água é ρ w = 1 M
A comporta AB possui 8 m de largura. Determine as componentes horizontal e vertical da força que atua sobre o pino em B e a reação vertical no suporte liso A; p = 1,0 Mg/m³.
109- Determine a força e o momento de reação no apoio A da viga em balanço que está submetida a carga distribuída mostrada.