Uma viga em balanço sustenta a carga variável mostrada. Calcule a força de sustentação e o momento em .
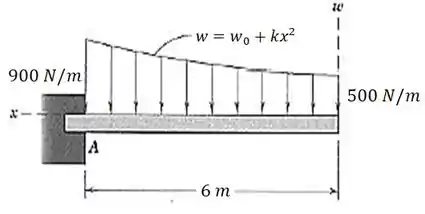
Passo 1
O diagrama de corpo livre desta viga fica assim:
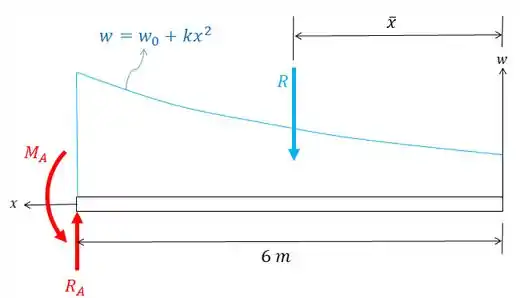
A equação de é dada por:
E esse na equação? Temos que descobrir o seu valor.
Quando temos que , então vamos substituir isso na nossa equação:
Quando temos que , então:
Assim, a nossa equação fica:
Passo 2
Para achar a força de reação , temos que calcular a resultante do carregamento distribuído. Para isso é só integrarmos a equação da curva ao longo do comprimento da viga:
Agora sim podemos achar a força de sustentação fazendo o equilíbrio de forças verticais:
Passo 3
Para calcular a coordenada centróide do carregamento distribuído vamos usar:
Assim:
O já sabemos que é:
Passo 4
Para achar o momento de reação no engaste, vamos fazer o somatório de momentos com relação ao ponto :
Vamos considerar o sentido de giro anti-horário com positivo. E repare que o braço de alavanca da resultante do carregamento distribuído é:
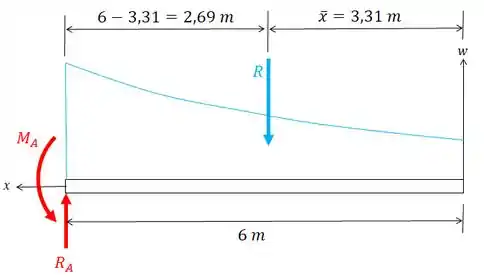
Então, o momento será: