Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Vigas – Efeitos externos

Ver Teoria
Exercício 51234678

Enunciado

Determine a força e o momento de reação em A para a viga que está submetida à combinação de carga mostrada.

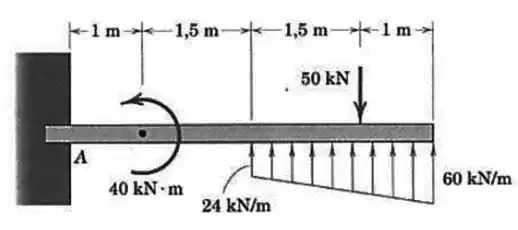
Passo 1

Vamos começar montando o diagrama de corpo livre:

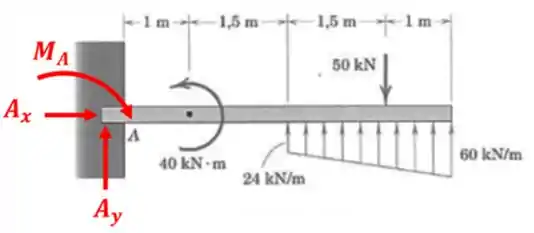
Repare que nossa força distribuída tem a forma de um trapézio. E o que fazemos quando isso acontece? Temos que dividir em um retângulo e um triângulo.

  • Retângulo: perceba que a força resultante tem o mesmo sentido das setinhas da carga distribuída, então nesse caso ela aponta para cima, desse jeito:

    • R 1   = 24 ( 2,5 ) = 60   k N

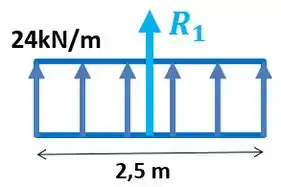
    Sabemos que a força resultante fica na metade do comprimento do retângulo:

    x - 1   = 1 2 ( 2,5 ) = 1,25   m

  • Triângulo:

R 2   = 36 ( 2,5 ) 2 = 45   k N

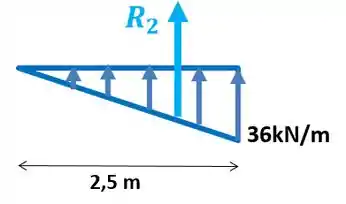
Essa força resultante fica localizada à 1 3 da altura do triângulo, então:

x - 2   = 1 3 2,5 = 1 3 5 2 = 5 6   m

Então, o nosso diagrama de corpo livre fica assim:

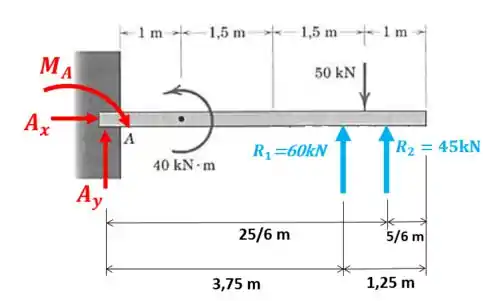
Passo 2

Agora temos escolher um ponto de referência para calcular os momentos. Vamos escolher o ponto A , porque esse ponto tem a maior quantidade de forças que são incógnitas.

∑ M A = 0 →   40 - 50 4 + 60 3,75 + 45 25 6 - M A = 0

M A = 252,5   k N m

Passo 3

Nosso próximo passo é fazer o somatório das forças. Repare que a única força horizontal é a nossa reação A x , logo ela será nula. Escrevendo matematicamente, temos:

∑ F x = 0   →   A x = 0

Agora vamos fazer o somatório das forças na vertical:

∑ F Y = 0   →   A y + 60 +   45 - 50 = 0

A y = - 55   k N

Resposta

A x = 0

A y = - 55   k N

M A = 252,5   k N m

Exercícios de Livros Relacionados

Se a massa do contrapeso em A é 6500k g , determine a força que a comporta exerce sobre o anteparo liso em C . A comporta é articulada em B e tem 1m de largura. A densidade da água é ρ w = 1M g / m 3
Determine a massa do contrapeso A se a comporta de 1m de largura está prestes a abrir quando a àgua está no nível mostrado. A comporta é articulada em B e mantida pelo anteparo liso em C . A densidade
A placa de aço elíptica B é usada para selar a abertura no tanque de armazenamento de água. Determine a intensidade da força hidrostática resultante que atua sobre ela. A densidade da água é ρ w = 1 M
A comporta AB possui 8 m de largura. Determine as componentes horizontal e vertical da força que atua sobre o pino em B e a reação vertical no suporte liso A; p = 1,0 Mg/m³.
109- Determine a força e o momento de reação no apoio A da viga em balanço que está submetida a carga distribuída mostrada.