A carga conectada em estrela desequilibrada da figura tem tensões equilibradas de e a sequência . Calcule as correntes de linha e a corrente neutra. Adote e .
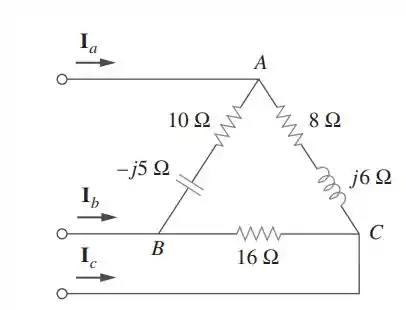
Passo 1
Essa é bem simples!
Vamos utilizar a Primeira Lei de Ohm para corrente alternada, ou seja, trabalhando com fasores:
Para :
Para :
Para :
Passo 2
Para achar a corrente de neutro: