Encontre as tensões de fase na carga para o sistema abaixo com fonte trifásica equilibrada e carga desequilibrada com:
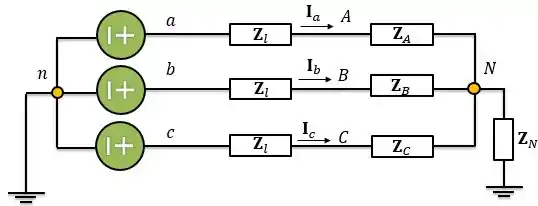
As impedâncias de cada linha são iguais e valem e a impedância do neutro é . Suponha que a sequência é e .
Passo 1
Esse circuito nada mais é do que um circuito com o neutro da carga aterrado por uma impedância. Temos que tomar cuidado porque temos que considerar a impedância da linha também. Vamos redesenhá-lo para a forma que conhecemos:
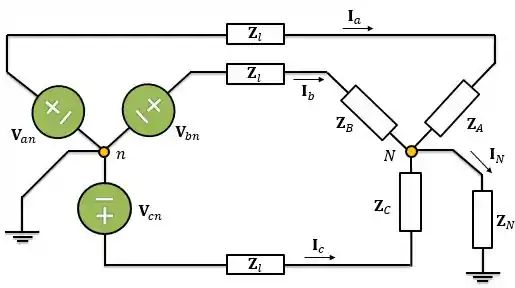
Como a sequência da fonte trifásica equilibrada é , temos:
Passo 2
Nesse circuito o neutro da carga não está diretamente ligado à terra. Ele está ligado a um resistor que está conectado à terra. Então, é como se existisse uma resistência entre o neutro da fonte e o neutro da carga .
Além disso, devido à presença desse resistor, temos que considerar a tensão entre o neutro da carga e a terra.
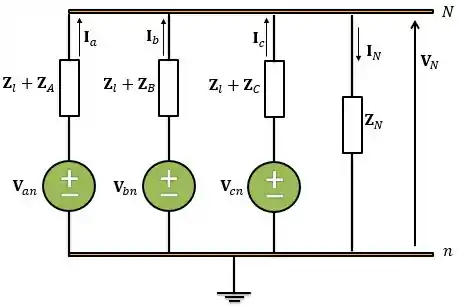
Onde:
Passo 3
Aplicando a LCK ao nó da carga, temos:
Agora vamos escrever as correntes em função das tensões:
Substituindo na equação nodal para determinarmos a tensão , temos:
Passo 4
Agora que temos a tensão entre os neutros, vamos calcular as correntes de linha:
Passo 5
Agora, finalmente podemos calcular as tensões de fase na carga. Para a fase , temos:
Para fase :
Para fase :