Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Análise de Circuitos Trifásicos Desequilibrados

Ver Teoria
Exercício 12345678910

Enunciado

Considere o sistema estrela-estrela com neutro da carga solidamente aterrado mostrado na figura abaixo.

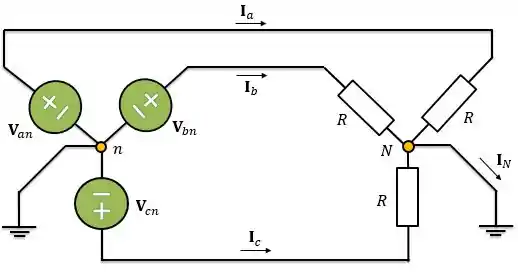
Adotando

V a n = 10 ∠ 0 °   V

V b n = 20 ∠ - 60 °   V

V c n = 20 ∠ 60 °   V

e que a carga trifásica é equilibrada com

R = 10   Ω

Determine as correntes de linha I a , I b , I c e   I n .

Passo 1

Como o neutro da carga está ligado à terra, seu potencial é zero e podemos desconsiderá-lo em nossa análise nodal.

V N = 0   V

Passo 2

Então, como os dois neutros estão ligados à terra podemos conectá-los e nossa análise fica assim:

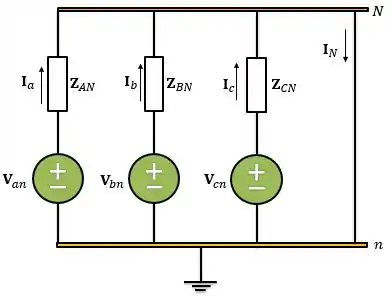
Aplicando a LCK ao nó da carga, temos:

I N = I a + I b + I c

Onde:

I a = V a n Z A N

I b = V b n Z B N

I c = V c n Z C N

Passo 3

Logo, utilizando os dados do enunciado:

V a n = 1 0 ∠ 0 °   V

V b n = 20 ∠ - 6 0 °   V

V c n = 20 ∠ 6 0 °   V

R = 1 0   Ω

As correntes serão de linha serão:

I a = 1 0 ∠ 0 ° 1 0 = 1 ∠ 0 °   A

I b = 20 ∠ - 6 0 ° 1 0 = 2 ∠ - 6 0 °   A

I c = 20 ∠ 6 0 ° 1 0 = 2 ∠ 6 0 °   A

Passo 4

Agora que temos as correntes de linha, vamos soma-las para encontrarmos a corrente que circula no neutro:

I N = 1 ∠ 0 ° + 2 ∠ - 60 ° + 2 ∠ 6 0 °

I N = 1 + 1 - j 1,73 2 + 1 + j 1,732

I N = 3   A

I N = 3 ∠ 0 °   A

Resposta

I a = 1 ∠ 0 °   A

I b = 2 ∠ - 60 °   A

I c = 2 ∠ 60 °   A

I N = 3 ∠ 0 °   A

Exercícios de Livros Relacionados

Use o PSpice ou MultiSim para determinar as correntes IaA e IaC no sistema trifásico desequilibrado mostrado na Figura 12.69. Seja Z l = 2 + j , Z 1 = 40 + j 20Ω Z 2 = 50 - j 30 Ω , Z 3 = 25Ω
Use o PSpice ou MultiSim para determinar Io no circuito monofásico trifilar da Figura 12.66. Seja Z 1 = 15-j 10Ω ,Z 2=30+j 20Ω eZ 3 = 12+j 5Ω .
Resolva o Problema 12.10 usando o PSpice ou MultiSim.
Considere a Figura 12.61 e elabore um problema que ajude outros estudantes a entender melhor sistemas trifásicos não equilibrados.
Um sistema trifásico quadrifilar operando com tensão de linha igual a 208V é mostrado na Figura 12.71. As tensões da fonte estão equilibradas. A potência absorvida pela carga resistiva conectada em es