Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Análise de Circuitos Trifásicos Desequilibrados

Ver Teoria
Exercício 21345678910

Enunciado

Para o circuito desequilibrado da figura, determine as correntes de linha

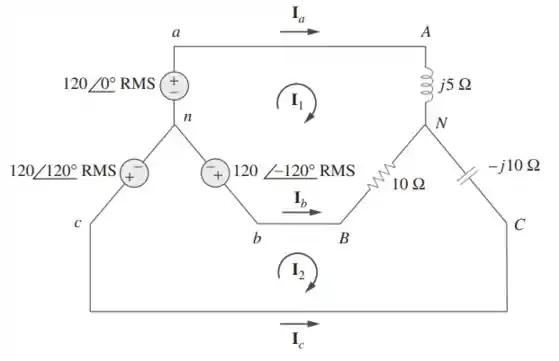
Passo 1

Vamos fazer a análise de malhas para encontrar as correntes necessárias.

Na malha 1:

120 ∠ - 120 ° - . 120 ∠ 0 ° + ( 10 + j 5 ) I 1 = 0

. ( 1 0 + j 5 ) I 1 - 10 I 2 = 120 3 . ∠ 30 °

Na malha 2:

120 ∠ 120 ° - . 120 ∠ - 120 ° + ( 10 - j 10 ) I 2 - 1 0 I 1 = 0

- 10 I 1 + ( 1 0 - j 10 ) I 2 = 120 3 . ∠ - 90 °

Passo 2

Vamos resolver esse sistema de equações (da malha 1 e da malha 2) na forma matricial:

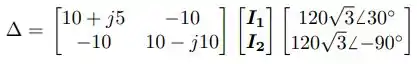
Agora, vamos achar primeiro o determinante dessa matriz e em seguida os determinantes das matrizes modificadas:

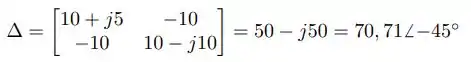
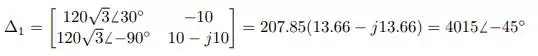
Passo 3

Para as correntes I 1 e I 2

I 1 = Δ 1 Δ = 4015.23 ∠ ° 70.71 ∠ - 45 ° = 56.78 A

I 2 = Δ 2 Δ = 3023.4 ∠ - 20.1 ° 70.71 ∠ - 45 ° = 42.75 ∠ 24.9 °

Para as correntes de linha teremos:

I a = I 1 = 56.78   A

I c =   - I 2 = 42.75 ∠ - 155.1 °   A

I b = I 2 - I 1 = 38.78 + j 18 - 56.78 = 25.46 ∠ 135 °   A

Passo 4

I a = 56.78   A

I c = 42.75 ∠ - 155.1 °   A

I b = 25.46 ∠ 135 °   A

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Use o PSpice ou MultiSim para determinar as correntes IaA e IaC no sistema trifásico desequilibrado mostrado na Figura 12.69. Seja Z l = 2 + j , Z 1 = 40 + j 20Ω Z 2 = 50 - j 30 Ω , Z 3 = 25Ω
Use o PSpice ou MultiSim para determinar Io no circuito monofásico trifilar da Figura 12.66. Seja Z 1 = 15-j 10Ω ,Z 2=30+j 20Ω eZ 3 = 12+j 5Ω .
Resolva o Problema 12.10 usando o PSpice ou MultiSim.
Considere a Figura 12.61 e elabore um problema que ajude outros estudantes a entender melhor sistemas trifásicos não equilibrados.
Um sistema trifásico quadrifilar operando com tensão de linha igual a 208V é mostrado na Figura 12.71. As tensões da fonte estão equilibradas. A potência absorvida pela carga resistiva conectada em es