Considere as funções:
E seja a região ilimitada definida por .
- Faça um esboço de
- Calcule a área de
Passo 1
Para o temos que as duas funções vão encontrar em:
Já para elas não encontram, pois .
Como todas essas funções são conhecidas, esboçamos:
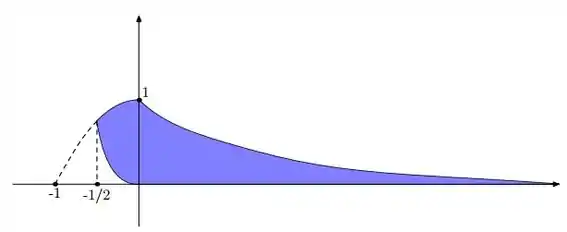
Passo 2
Temos que separar a integral em duas regiões:
Resolvendo, podemos integrar termo à termo:
Substituindo os valores:
Passo 3
Já a outra:
Segue que área é a soma desses dois resultados:
Resposta
Exercícios de Livros Relacionados
Esboce a região e encontre sua área (se a área for finita). S = x , y x ≥ 0 ,0 ≤ y ≤ x x 2 + 9 }
Esboce a região e encontre sua área (se a área for finita). S = x ,y ; x ≥ 1 ,0 ≤ y ≤ e - x
Se g x = 1 x - 1 , use sua calculadora ou computador para fazer uma tabela de valores aproximados de ∫ 2 t g x d x para t = 5 , 10 , 100 , 1000 e 10000 . Parece que ∫ 2 ∞ g x d x é convergente ou dive
Esboce a região e encontre sua área (se for finita) x , y ; x ≥ 1,0 ≤ y ≤ 1 x 3 + x
Esboce a região e encontre sua área (se a área for finita). S = x , y 0 ≤ x ≤ π 2 ,0 ≤ y ≤ sec 2 x }