Q01) Seja a função definida por , cujo gráfico está esboçado abaixo:

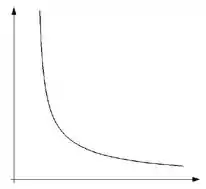
Considere a seguinte região plana:

Sabendo que as retas e são assíntotas do gráfico de , faça o que se pede

1. Escreva a área da região como uma integral na variável . Neste item não é necessário calcular a integral
2. Calcule a área da região e conclua que ela é infinita

Pra calcular essa área, primeiro vamos lembrar o seguinte: essa forma de escrever está errada! Pro professor não ficar bravo, é sempre bom reescrever na prova a forma certa:

Agora temos três etapas:

• Integrar de forma indefinida
• Aplicar os limites de integração
• Aplicar o limite

Vamos por a mão na massa então! Pra primeira etapa, uma boa ideia é olhar bem pro interior da integral: é um polinômio dividido por outro né? E o do denominaor é uma diferença de quadrados! Não sei vocês mas isso me cheira a resolução por frações parciais. Abrindo o produto notável, temos:

Das igualdades acima, vou pegar só a segunda e a última agora, mas comparar só o que ta dentro da integral. Olha só:

Colocando tudo no mesmo denominador, temos:

Cortando o denominador dos dois lados e aplicando a distributiva, ficamos com:

Agrupando os termos em comum..:

Oras, da então pra montar um sistema de equações! Olha só como fica:

Somando as duas equações, chegamos a:

E sabendo , chegamos a . Resumimos a integral à:

O que é uma integral com resolução direta em! Vai dar:

Agora que a gente vai começar a falar de limites. Primeiro os limites de integração. Vamos ter:

O que por fim, dá:

Aplicando o limite agora , temos:

Concluímos então que a área é infinita ;)