Área entre Curvas
Considere a região delimitada pelas curvas e , para .
Determine a área da região no caso .
Determine o valor de para que a área de seja o dobro da obtida no item anterior.
Passo 1
Começamos, como sempre, esboçando esse espaço aí que o cara deu:
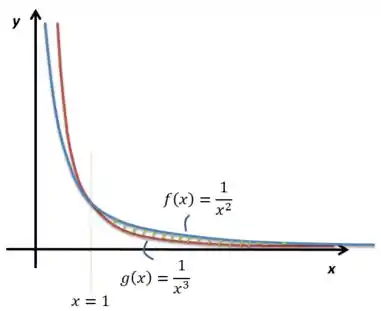
Bom, os gráficos só se tocam em , então para achar a área entre eles eu preciso resolver uma integral imprópria. Para , é sempre maior que . Assim, o cálculo da integral se resume a isso aqui:
Passo 2
Bom, agora além da área depois de , que vale pelo que achamos na letra , temos que somar uma área entre os gráficos que vai de até . Ou seja,
Onde é a área de até
Nesse espaço, , pode substituir uns valores para comprovar isso. Redesenhando as duas hipérboles, teríamos isso aqui:
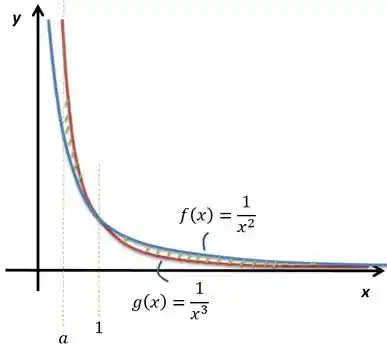
Ele quer
Então
Vamos ter a seguinte integral então
Desses dois valores, um não pode. Lembra, no enunciado ele pede que seja maior que . Assim, o que procuramos é !