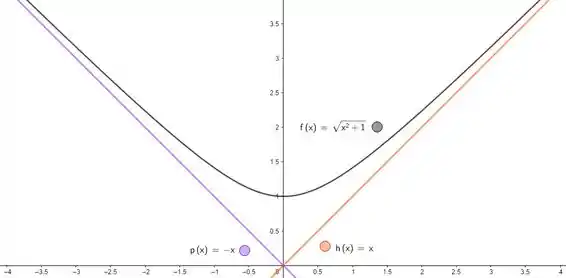
Seja . Determine todas as assíntotas de .
Passo 1
Primeiro, vamos analisar o domínio. Nesse caso, não vamos ter nenhum problema porque não há nenhum valor de que nossa função não aceite, beleza? Em matematiquês, é o mesmo que dizer que não temos indeterminações.
E olha só! Se não temos indeterminações, não vamos ter candidatos à assíntotas verticais!
Passo 2
Vamos procurar agora assíntotas horizontais. Para isso, vamos jogar nosso limite para e , tranquilo?
E saca só, o está ao quadrado! Então já sabemos que não tem como o interior dessa raiz ser um número negativo! Não importa se ou o limite vai ser sempre:
Então descartamos também a possibilidade de termos assíntotas horizontais!
Passo 3
Quando temos assíntotas horizontais para e/ou para , temos a certeza que não existem assíntotas oblíquas. Como nesse caso não temos nem assíntotas verticais nem horizontais, vamos checar pra ver se a gente acha oblíquas? Simbora:
Seja , é só calcular agora. Pro coeficiente angular primeiro, ficamos com:
Pra resolver esse limite, saca só esse conceito importante aqui:
Pra , temos que , então . Sendo assim:
Pra , temos que , então . Sendo assim:
Opa, se temos dois valores de diferentes então temos duas assíntotas oblíquas diferentes! Já que é assim, vamos usar valores diferentes de no cálculo de . Para , usamos . Logo, calculamos :
Multiplicando pelo conjugado:
E, pra fechar com chave de ouro, usando , temos que . Logo, calculamos :
Multiplicando pelo conjugado:
Opa, se o tanto pra quanto pra , nossas duas assíntotas oblíquas vão ser:
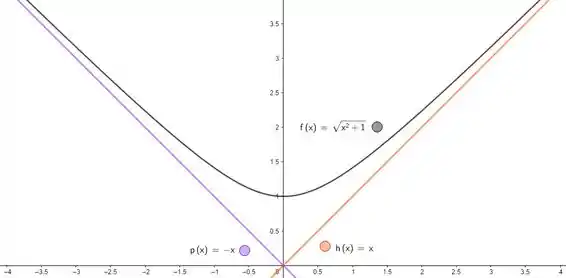
Resposta