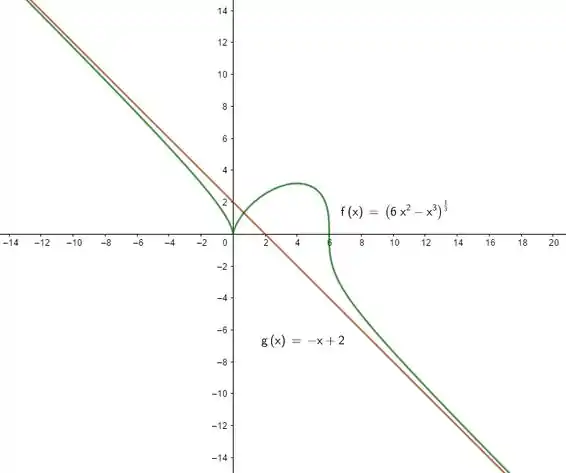
Seja . Determine a(s) assíntota(s) oblíqua(s) de .
Passo 1
Essa questão já ta nos dizendo que tem pelo menos uma assíntota oblíqua, então já nem precisamos nos preocupar em achar outras assíntotas. Então nesse passo, vamos desenrolar esse enunciado e escrever . Saca só:
Passo 2
Vamos lembrar que as assíntotas oblíquas são definidas por:
Então, uma coisa de cada vez se não a gente se afoba. Primeiro achamos , depois . O cálculo de vai ficar:
Se a gente colocar no numerador o
Passo 3
Agora vamos calcular o valor de . Felizmente só vamos ter pra nos preocuparmos já que também só achamos . Como , calculamos o da seguinte forma:
Puts, esse limite parece complicado. Mas olha um detalhe importante dele: a raiz cúbica! Ela atrapalha, não é mesmo? Que tal tentarmos tirar ela daí usando esse produto notável:
Se fizermos e , multiplicando em cima e em baixo por temos:
Show de bola, numerador simplificado. Agora vamos simplificar o denominador. Vamos abrir o termo :
E colocando em evidência:
Agora, colocando em evidência em , ficamos com:
Jogando isso dentro do denominador:
Colocando em evidência:
E, finalmente, aplicando o limite:
Ufa, cabou! A assíntota oblíqua será então:
Resposta