Um cilindro de comprimento e raio é feito de uma mistura complexa de materiais. Sua resistividade depende da distância da extremidade esquerda e obedece à fórmula
em que e são constantes. Na extremidade esquerda, a resistividade é de , e a do lado direito é de .
- Qual é a resistência desse bastão?
- Qual é o campo elétrico na metade do seu comprimento, se ele carregar uma corrente de ?
- Se cortarmos o bastao em dois segmentos de , qual é a resistência de cada metade?
Passo 1
a) De acordo com a Figura abaixo, a resistência infinitesimal pode ser escrita como
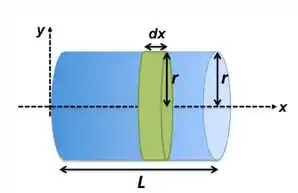
Onde a area é a área da seção reta do cilindro que é um círculo:
Agora, repara que a gente não conhece os valores das constantes e . Para encontrá-los, sabemos, pelo enunciado, que
e que
Resolvendo a última equação acima utilizando o valor de obtido com , temos
Portanto,
Essa é a nossa expressão para a resistividade!
Passo 2
Substituindo os valores das constantes na integral e integrando em todo o comprimento do cilindro teremos:
onde tiramos o da integral, pois esse valor é fixo ao longo de todo o cilindro. Ok? Fica atento, porque se fosse um tronco de cone, por exemplo, esse raio poderia variar ao longo do eixo . Mas aqui neste caso, é fixo, o que facilita nossa vida…
Continuando com a integral acima, quando a resolvemos, obtemos que a resistência total do cilindro é
Substituindo os valores do raio do cilindro e do comprimento , encontramos o valor da resistência .
Passo 3
Passo 4
b) A gente viu que a lei de Ohm mostra que , ou seja, ela mostra uma relação de proporcionalidade entre o campo elétrico e densidade de corrente . Mas o que precisamos encontrar neste item é o campo no ponto , que é dado por
Portanto, como foi um valor dado e conhecemos a área, só precisamos encontrar a resistividade nesse ponto:
E substituindo o valor do comprimento teremos:
E assim, encontramos o campo elétrico
E substituindo o raio do cilindro e a corrente , teremos:
Passo 5
c) Considerando que a primeira metade do cilindro tem resistência , teremos que mudar o limite superior de integração lá do Passo 1 para obter que
Substituindo os valores do enunciado, teremos que
Essa é a resistência da primeira metade do cilindro.
Agora, para obter qual é a resistência da segunda metade do cilindro que vai de a , a gente precisa subtrair da resistência total , ou seja,
Portanto, a segunda metade tem uma resistência maior que a primeira.
É claro que uma outra alternativa aqui é pegar a integral lá do Passo 1 e mudar o limite inferior de integração para e o limite superior para . Isso tem que dar o mesmo valor que a gente obteve acima e é uma boa forma de você também treinar o raciocínio.