A região entre duas esferas concêntricas condutoras com raios e está preenchida por um material condutor com resistividade constante.
a) Mostre que a resistência entre as esferas é dada por
b) Deduza uma expressão para a densidade de corrente em função do raio em termos da diferença de potencial entre as esferas.
c) Mostre que o resultado da parte (a) se reduz a
quando a distância entre as esferas é pequena.
Passo 1
a) A situação que a gente tem nesse caso é dado na Figura abaixo. Se a corrente atravessa a região entre as esferas condutoras no sentido radial, então ela atravessa uma área de e um elemento de comprimento.
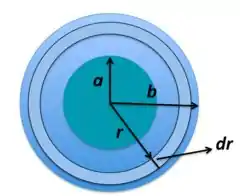
Por isso, ao atravessar esse comprimento com área , a resistência oferecida à corrente nesse trajeto é dada por
Agora, para sabermos a resistência total, temos que integrar de , raio da esfera interna, até , que é o raio da esfera externa e isso nos dá que
Simplificando um pouco mais a expressão anterior, temos
Passo 2
b) Sabemos que a densidade de corrente é dada por , sendo que ( ) é o raio de superfície esférica através da qual a corrente passa.
Mas, como e temos a resistência dada no item (a), a densidade de corrente pode ser reescrita como
expressão que simplificada resulta em
Passo 3
c) Fazendo a distância pequena, temos que a resistência total é dada por
em que é a área da esfera interna.