Um resistor com resistividade , tem a forma de um cilindro oco de comprimento e raios e . Calcule a resistência e o módulo do vetor densidade de corrente no interior do resistor nos casos em que uma diferença de potencial é aplicada:
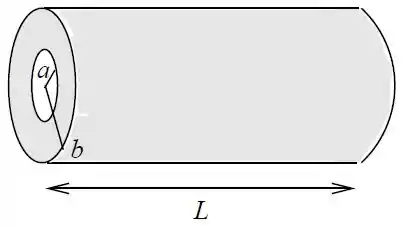
entre as bases do cilindro.
entre as superfícies interna de raio e a externa de raio .
Passo 1
entre as bases do cilindro.
Por definição, a resistência de um capacitor é dada por:
Nesse caro, será a área da coroa circular de raios e .
Portanto:
Passo 2
Por definição, a densidade de corrente é dada por:
Usando a Lei de Ohm, podemos dizer que:
Resta agora substituir a resistência que achamos no passo anterior:
Passo 3
entre as superfícies interna de raio e a externa de raio .
A ideia aqui é bem parecida com o que fizemos antes, a diferença é que, como a corrente agora flui radialmente, vamos ter que mudar a forma de calcular a resistência.
Vamos começar dividindo o cilindro em camadas cilíndricas de largura . Cada cilindro terá resistência , dada por:
agora será a área lateral do cilindro.
Logo:
Pra encontrar uma expressão pra , precisamos integrar esse cara, onde :
Passo 4
Pra calcular a densidade de corrente, vamos usar a mesma ideia que usamos anteriormente:
Só que agora vamos usar a nova resistência calculada:
Resposta