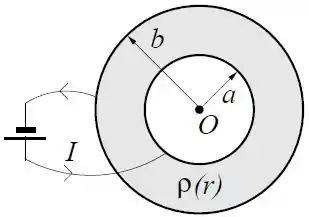
A região entre duas cascas esféricas condutoras concêntricas de raios e com é preenchida com um material de resistividade elétrica , onde é a distância até o centro das cascas esféricas e é uma constante.
Ligando-se uma bateria às cascas esféricas como na figura observa-se uma corrente no sentido indicado.
- Calcule o vetor densidade de corrente na região entre as cascas .
- Usando a lei de Ohm, determine o vetor campo elétrico entre as cascas esféricas.
- Calcule a resistência desse sistema em função de , e .
Passo 1
- Calcule o vetor densidade de corrente na região entre as cascas .
- Usando a lei de Ohm, determine o vetor campo elétrico entre as cascas esféricas.
- Calcule a resistência desse sistema em função de , e .
Sabendo que a corrente sai da placa maior da fonte (ali na esquerda da figura), corre o circuito e volta para a placa menor, a gente consegue ver que a corrente vai fluir da casca menor para a casca maior.
Beleza! Além disso, a densidade de corrente está relacionada com a corrente através da seguinte equação:
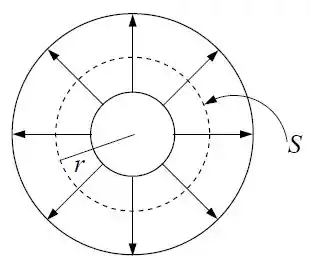
Agora é só resolver a integral e acabou!
Já sabemos que a resistividade depende de ... logo, a densidade de corrente também vai depender de .
A integral vai ser exatamente a área da superfície , de raio . Portanto:
Ah! Você só não pode esquecer de um detalhe muito importante... o problema pediu pra calcular o vetor densidade de corrente. Então faltou especificarmos a direção e o sentido da corrente.
A parada é que nós acabamos falando disso aqui em cima. Quando falamos que a corrente vai fluir da casca esférica menor para a casca esférica maior, no fundo nós falamos que a densidade de corrente tem a direção radial, apontando pra fora... do mesmo jeito que representamos na última figura.
Portanto:
Passo 2
Vamos lá! A lei de Ohm nos permite relacionar a densidade de corrente com o campo elétrico através da seguinte equação:
Onde é a resistividade. Agora ficou fácil para nós!
Só vamos ter o trabalho de substituir o que o problema nos disse e o que achamos no passo 1.
Passo 3
Beleza... o melhor caminho pra calcular essa resistência é através da relação:
Mas pra isso nós temos que encontrar a diferença de potencial . Pô! Mas na letra (b) nós calculamos o campo elétrico, certo?
Show! Podemos relacionar o campo elétrico com o potencial pela expressão:
Voltando pra nossa primeira relação: