Considere uma camada esférica condutora de raio interno e raio externo , conforme a figura.

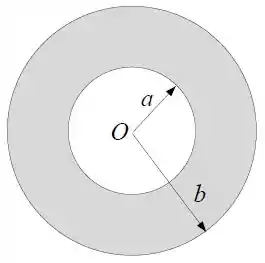
A resistividade da camada cresce linearmente com a distância ao centro , sendo dada por

Onde é uma constante positiva.

Determine a dimensão da constante no Sistema Internacional de Unidades.

Calcule a resistência elétrica da camada esférica na direção radial.

Uma diferença de potencial é aplicada entre as duas superfícies. Supondo que o potencial maior seja o da superfície interna, calcule a corrente e o vetor densidade de corrente.

Calcule a resistência elétrica da camada esférica na direção radial.

Como essa geometria é diferente da qual estamos acostumados, vamos começar pensando em uma camada infinitesimal, de resistência , espessura e área . Pela definição de resistência:

Agora ficou mais tranquilo... só temos que integrar esse cara nos limites .

O problema já nos disse que , logo, substituindo na expressão acima:

Uma diferença de potencial é aplicada entre as duas superfícies. Supondo que o potencial maior seja o da superfície interna, calcule a corrente e o vetor densidade de corrente.

Opa! Pra calcular a corrente ficou tranquilo, porque já temos a resistência e o problema falou da diferença de potencial .

Então é só usar a Lei de Ohm e ser feliz.

Se o potencial maior é o da superfície interna, isso quer dizer que a corrente flui da superfície interna para a superfície externa... isso que dizer que o vetor densidade de corrente vai estar na direção radial, de dentro para fora.

Por definição, a densidade de corrente é dada por:

Como aqui a área vai depender do raio , basta substituir isso na fórmula acima.

Logo:

Pra finalizar, basta substituir aqui a expressão que encontramos para a corrente ali em cima.

Simplificando: