Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Resistência com Integrais

Ver Teoria
Exercício 101234567891112

Enunciado

UFMG – Fundamentos de Eletromagnetismo – P2 – Questão 3

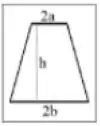
A figura abaixo mostra um cone feito de cobre com resistividade ρ , com a ponta aparada por um plano paralelo à base. As duas faces circulares do corpo têm raios a e b , e a distância entre as bases é igual a h .

  1. Encontre a expressão literal para resistência elétrica entre essas faces.
  2. Substitua os valores de a = 1 m m , b = 10 m m , h = 1 m , e considerando ρ c o b r e = 1,67 × 10 - 8 Ω m , encontre o valor correto.

Passo 1

Oi, tudo bem?

Essa questão parece complicada, mas vou ajudar você aqui! Vamos lá?

Letra (a):

Precisamos calcular a resistência desse cone cortado em cima! É como se fosse um chapeuzinho de aniversário de cobre, cortado em cima

Para calcular a resistência, vamos utilizar a fórmula que nos dá R em termos da área e do comprimento do resistor:

R = ρ L A

Bom, como não temos um fio de seção reta constante, precisamos integrar! E para isso, precisamos relacionar o diferencial e comprimento (no nosso caso a altura h ) com a área do cone (vai da área da base – círculo de raio b , e o topo – círculo de raio a )

Então, temos que o raio do cone é r = b para y = 0 e temos que r = a quando y = h . Taí nossa amarração da área com a altura!

O diferencial de resistência é

d R = ρ d y A

Beleza? Agora precisamos encontrar a dependência do raio r com a área e com os valores de a , b , h .

Passo 2

Olhando com mais carinho para nosso cone, podemos fazer essas comparações:

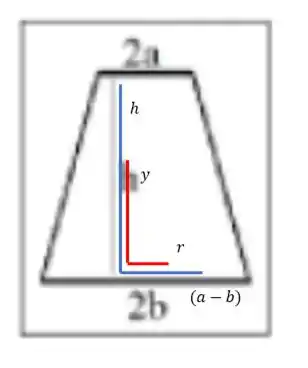
Que podemos encontrar a seguinte relação:

y r = h a - b

E r em termos de a , b , h é:

r = a - b y h

E a área? Bom, a área da base de um cone é a de um círculo de raio r ' = r + b :

A = π r 2 = π a - b y h + b 2

E essa expressão é que vamos substituir no d R do passo anterior:

d R = ρ d y A = ρ d y π a - b y h + b 2

E a resistência vai ser a integral dessa expressão:

R = ∫ ρ d y π a - b y h + b 2

Tudo bem até aqui?

Calma, vamos facilitar um pouco!

Passo 3

E da relação que tiramos entre r e y :

r = a - b y h

Podemos relacionar os diferenciais:

d r = a - b h d y

E podemos substituir na integral:

R = ∫ b a ρ h ( a - b ) d r π r 2

Agora trocamos tudo por r ! Muito mais fácil de resolver!

r temos:

R = ρ h a - b π - 1 r b a = ρ h a - b π 1 b - 1 a

Agora é só manipular um pouco esse resultado para simplificar:

R = ρ h a - b π a - b b a = ρ h b a π

Passo 4

Letra (b): com a expressão da resistência na mão, podemos substituir os valores e correr para o abraço!

Os valores dados são:

a = 1 m m , b = 10 m m , h = 1 m , e considerando ρ c o b r e = 1,67 × 10 - 8 Ω m ,

Agora é só substituir:

R = ρ h b a π = 1,67 × 10 - 8 . 1 1 × 10 - 3 . 10 × 10 - 3 . π = 5,32 × 10 - 4 Ω

Beleza?

Espero ter ajudado!

Vamos para a próxima?

Resposta

5,32 × 10 - 4 Ω

Exercícios de Livros Relacionados

O carbono tem um coeficiente de temperatura de resistividade negativo. Isso significa que a sua resistividade cai quando sua temperatura aumenta. Sua resistividade desapareceria completamente para alg