Uma esfera condutora de raio está no interior de uma casca esférica fina condutora de raio . A esfera e a casca esférica são concêntricas e o espaço entre elas está preenchido com um material de resistividade constante, conforme a figura. Uma corrente elétrica , uniformemente distribuída através do material entre os condutores, flui da esfera interna para a casca esférica.
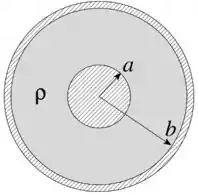
(a) Determine o vetor densidade de corrente na região entre os condutores ().
(b) Calcule a diferença de potencial entre os condutores.
(c) Calcule a resistência elétrica entre os condutores.
(d) Calcule a resistência entre os condutores no limite em que .
Passo 1
Sabemos que a corrente elétrica é o fluxo da densidade de corrente por uma certa superfície. Como a corrente flui da esfera interna para a esfera externa, temos que a densidade de corrente deve estar na direção radial, ou seja, .
Pelo enunciado temos também que corrente elétrica é uniforme, ou seja, o fluxo da densidade de corrente por uma esfera de raio () será .
Assim a corrente é dada por
onde teremos . Assim
Passo 2
Como já sabemos a densidade de corrente na região entre os condutores e sabemos a resistividade do material nessa região podemos calcular o campo elétrico usando a lei de Ohm com a sua cara menos simpática
Passo 3
Agora que temos o campo elétrico nessa região, podemos calcular a diferença de potencial
O módulo da diferença de potencial será dado por
Passo 4
Para calcular a resistência entre os condutores vamos usar a lei de Ohm com a sua cara mais simpática
Passo 5
Agora temos que calcular a resistência no limite de . Para ver como ficaria, é só separar cada termo na resistência
No limite de só o segundo termo irá para . Assim