Considere dois eletrodos esféricos concêntricos de raios e , conforme a figura. O meio resistivo entre os eletrodos é homogêneo com condutividade . Uma corrente flui do eletrodo interno de raio para o eletrodo externo de raio através do meio resistivo.
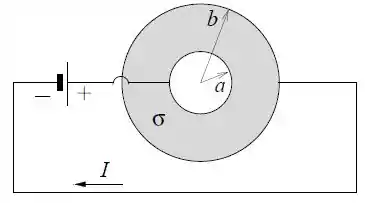
- Calcule, em função da corrente , o vetor densidade de corrente no meio resistivo a uma distância do centro dos eletrodos .
- Calcule a resistência do sistema ôhmico em função de , e .
- Qual o valor da diferença de potencial entre os eletrodos em função de , , e ?
Passo 1
- Calcule, em função da corrente , o vetor densidade de corrente no meio resistivo a uma distância do centro dos eletrodos .
- Calcule a resistência do sistema ôhmico em função de , e .
- Qual o valor da diferença de potencial entre os eletrodos em função de , , e ?
Sabendo que a corrente sai da placa maior da fonte (ali na esquerda da figura), corre o circuito e volta para a placa menor, a gente consegue ver que a corrente vai fluir da casca menor para a casca maior.
Beleza! Além disso, a densidade de corrente está relacionada com a corrente através da seguinte equação:
Agora é só resolver a integral e acabou!
Já sabemos que a resistividade depende de ... logo, a densidade de corrente também vai depender de .
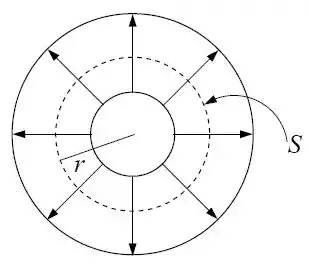
A integral vai ser exatamente a área da superfície , de raio . Portanto:
Ah! Você só não pode esquecer de um detalhe muito importante... o problema pediu pra calcular o vetor densidade de corrente. Então faltou especificarmos a direção e o sentido da corrente.
A parada é que nós acabamos falando disso aqui em cima. Quando falamos que a corrente vai fluir da casca esférica menor para a casca esférica maior, no fundo nós falamos que a densidade de corrente tem a direção radial, apontando pra fora... do mesmo jeito que representamos na última figura.
Portanto:
Passo 2
Por definição, a condutividade é o inverso da resistividade:
Então basta usar a própria definição de resistência aqui:
Como estamos falando de cascas esféricas, , voltando pra fórmula acima:
Passo 3
Agora não tem muito erro... sabemos que ali passa uma corrente e logo ali em cima nós calculamos a resistência... então basta usar a relação: