Exercícios de Cálculo de Resistência com Integrais - Lista de Exercícios Resolvida

Na figura abaixo uma corrente elétrica atravessa um tronco de cone circular reto de resistividade , raio menor , raio maior e comprimento . A densidade de corrente é uniforme ao longo de uma seção reta perpendicular ao eixo do objeto. Qual é a resistência do objeto?

Um cilindro de comprimento e raio é feito de uma mistura complexa de materiais. Sua resistividade depende da distância da extremidade esquerda e obedece à fórmula

em que e são constantes. Na extremidade esquerda, a resistividade é de , e a do lado direito é de .

1. Qual é a resistência desse bastão?
2. Qual é o campo elétrico na metade do seu comprimento, se ele carregar uma corrente de ?
3. Se cortarmos o bastao em dois segmentos de , qual é a resistência de cada metade?

Considere uma camada esférica condutora de raio interno e raio externo , conforme a figura.

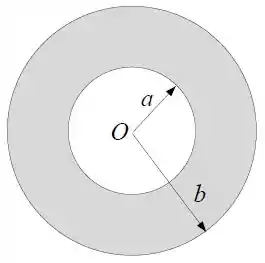
A resistividade da camada cresce linearmente com a distância ao centro , sendo dada por

Onde é uma constante positiva.

Determine a dimensão da constante no Sistema Internacional de Unidades.

Calcule a resistência elétrica da camada esférica na direção radial.

Uma diferença de potencial é aplicada entre as duas superfícies. Supondo que o potencial maior seja o da superfície interna, calcule a corrente e o vetor densidade de corrente.

A região entre duas esferas concêntricas condutoras com raios e está preenchida por um material condutor com resistividade constante.

a) Mostre que a resistência entre as esferas é dada por

b) Deduza uma expressão para a densidade de corrente em função do raio em termos da diferença de potencial entre as esferas.

c) Mostre que o resultado da parte (a) se reduz a

quando a distância entre as esferas é pequena.

A resistividade de um semicondutor pode ser alterada adionando-se diferentes quantidades de impurezas. Uma barra de um semicondutor de comprimento e seção reta de área está ao longo do eixo , entre e . O material obedece à lei de Ohm e sua resistividade varia ao longo da barra, de acordo com a relação

A extremidade da barra para está a um potencial mais elevado do que o potencial da extremidade .

1. Calcule a resistência total da barra e a corrente que flui através dela.
2. Determine o módulo do campo elétrico na barra em função de .
3. Calcule o potencial .

Um resistor com resistividade , tem a forma de um cilindro oco de comprimento e raios e . Calcule a resistência e o módulo do vetor densidade de corrente no interior do resistor nos casos em que uma diferença de potencial é aplicada:

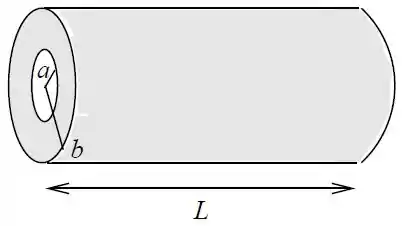
entre as bases do cilindro.

entre as superfícies interna de raio e a externa de raio .

A região entre duas cascas esféricas condutoras concêntricas de raios e com é preenchida com um material de resistividade elétrica , onde é a distância até o centro das cascas esféricas e é uma constante.

Ligando-se uma bateria às cascas esféricas como na figura observa-se uma corrente no sentido indicado.

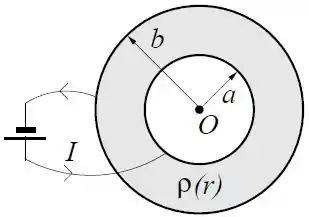
1. Calcule o vetor densidade de corrente na região entre as cascas .
2. Usando a lei de Ohm, determine o vetor campo elétrico entre as cascas esféricas.
3. Calcule a resistência desse sistema em função de , e .

Considere uma camada esférica condutora de raio interno e raio externo , conforme a figura.

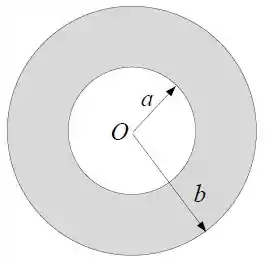
A resistividade da camada cresce linearmente com a distância ao centro , sendo dada por

Onde é uma constante positiva.

Determine a dimensão da constante no Sistema Internacional de Unidades.

Calcule a resistência elétrica da camada esférica na direção radial.

Uma diferença de potencial é aplicada entre as duas superfícies. Supondo que o potencial maior seja o da superfície interna, calcule a corrente e o vetor densidade de corrente.

Uma esfera condutora de raio está no interior de uma casca esférica fina condutora de raio . A esfera e a casca esférica são concêntricas e o espaço entre elas está preenchido com um material de resistividade constante, conforme a figura. Uma corrente elétrica , uniformemente distribuída através do material entre os condutores, flui da esfera interna para a casca esférica.

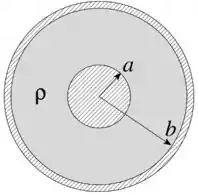
(a) Determine o vetor densidade de corrente na região entre os condutores ().

(b) Calcule a diferença de potencial entre os condutores.

(c) Calcule a resistência elétrica entre os condutores.

(d) Calcule a resistência entre os condutores no limite em que .

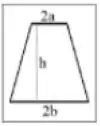
A figura abaixo mostra um cone feito de cobre com resistividade , com a ponta aparada por um plano paralelo à base. As duas faces circulares do corpo têm raios e , e a distância entre as bases é igual a .

1. Encontre a expressão literal para resistência elétrica entre essas faces.
2. Substitua os valores de , , , e considerando , encontre o valor correto.

Considere dois eletrodos esféricos concêntricos de raios e , conforme a figura. O meio resistivo entre os eletrodos é homogêneo com condutividade . Uma corrente flui do eletrodo interno de raio para o eletrodo externo de raio através do meio resistivo.

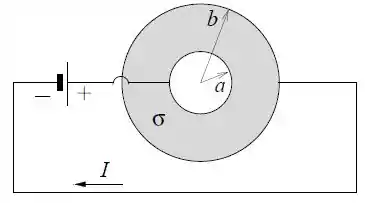
1. Calcule, em função da corrente , o vetor densidade de corrente no meio resistivo a uma distância do centro dos eletrodos .
2. Calcule a resistência do sistema ôhmico em função de , e .
3. Qual o valor da diferença de potencial entre os eletrodos em função de , , e ?

Um resistor com resistividade , tem a forma de um cilindro oco de comprimento e raios e . Calcule a resistência e o módulo do vetor densidade de corrente no interior do resistor nos casos em que uma diferença de potencial é aplicada:

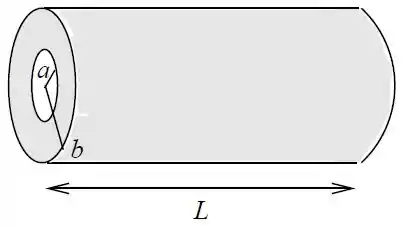
entre as bases do cilindro.

entre as superfícies interna de raio e a externa de raio .