Exercícios Resolvidos de Cálculo do Potencial a partir do Campo Elétrico

Enunciado

Um cilindro condutor infinito ao longo do eixo de raio tem densidade de carga constante . Calcule o potencial a uma distância do eixo do cilindro, dado que a uma distância ele vale . O potencial dado poderia ter sido no infinito?

Passo 1

Rascunhando a situação, temos:

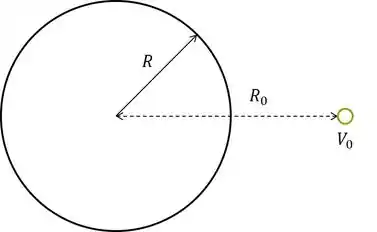
Como essa questão é a cara da Lei de Gauss para calcular o campo, vamos preferir utilizar a fórmula:

Escolhendo um caminho radial em direção ao cilindro. Estabelecido isso, vamos partir para calcular o campo. enunciando a Lei de Gauss:

Pela simetria cilíndrica do problema, escolhemos uma Gaussiana cilíndrica de raio arbitrário e comprimento arbitrário . Dado que escolhemos uma superfície com essas dimensões e já aproveitamos a simetria do campo, temos que o vetores normais à parte lateral da superfície são paralelos ao campo, ao passo que os vetores normais nas tampas são perpendiculares a ele, de forma que:

De forma que:

Portanto:

Passo 2

Pela configuração do campo, o seu módulo é constante em toda parte lateral da Gaussiana:

E temos então a área da lateral com nossa integral:

A expressão para a área lateral é dada pela fórmula:

Logo, temos:

Passo 3

Temos uma densidade linear constante, portanto é válido dizer que a razão entre a carga interna à Gaussiana e o comprimento dela é igual à densidade:

Logo temos:

Substituindo na expressão do campo:

Ainda pela questão da simetria, temos que o campo vai ter somente essa componente radial, então:

Passo 4

Partindo do ponto dado para um ponto arbitrário com distância até o centro, escolhemos um caminho qualquer.

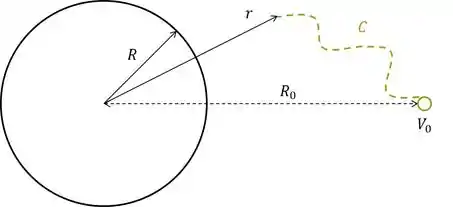
O caminho pode sim ser qualquer um, como na figura, mas se você quiser evitar do examinador da prova exigir uma demonstração desse fato, talvez você queira particularizar e dizer que o caminho é radial, daí nesse caso temos que o campo e o seu vetor são sempre paralelos ao longo do caminho. Aplicando na fórmula, temos: