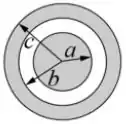
Q - Uma esfera não-condutora de raio , carregada com carga , é envolvida por uma camada esférica condutora, de raio interno e raio externo , carregada com uma carga .
Encontre o vetor campo elétrico para todos os pontos do espaço .
Calcule o potencial elétrico para todos os pontos do espaço . Considere em .
Qual o trabalho realizado pelo campo elétrico para mover uma carga de prova entre os pontos e ? Justifique sua resposta e lembre-se que o sinal tem significado físico.
Passo 1
Vem comigo que a gente vai se livrar dessa juntos!
Para encontrar o campo elétrico em cada ponto do espaço vamos usar a lei de Gauss ao nosso favor, dada por:
Onde é a superfície Gaussiana que vamos utilizar para envolver a região que vamos analisar.
Para achar o potencial em todas a regiões vamos usar a seguinte equação:
Onde vai ter que ser em coordenadas esféricas devido a ao fato de estarmos lidando com esferas.
Agora o trabalho pedido podemos encontrar da seguinte forma:
Passo 2
Vamos começar encontrando o campo na região .
Vamos considerar uma esfera gaussiana com raio , vamos aplicar a lei de Gauss para essa superfície, temos:
Onde é a carga dentro dessa superfície que traçamos. Mas como descobrir quanto vale essa carga?
Então, a carga é distribuída uniformemente na esfera de raio então a densidade de carga por volume é a mesma em qualquer ponto da esfera, assim temos que:
Então temos que:
Agora olhando a integral do lado esquerdo, podemos colocar para fora dela já que não tem motivo para esse campo não ser homogêneo ao longo da superfície, já que ele é radial. Então:
A integral de nos fornece a área da superfície gaussiana que consideremos, assim:
Como podemos ver para o campo cresce a medida que aumenta.
Passo 3
Agora vamos considerar a região .
Vamos de novo considerar uma superfície Gaussiana com um raio , vamos aplicar a lei de Gauss para essa superfície, temos:
A carga dentro da nossa superfície nesse caso é carga da esfera, então:
Com isso, ficamos com:
Podemos jogar para fora da integral pelo mesmo motivo de antes, com isso temos que:
Então temos que o campo nessa região é dado por:
Podemos ver que o campo cai com nessa região.
Passo 4
Agora vamos considerar a região .
Nessa região estamos dentro do condutor, então temos que o campo elétrico nessa região é zero, já que isso é uma característica dos condutores.
Agora a região .
Vamos fazer o mesmo processo que fizemos nas outras regiões, vamos considerar uma gaussiana com raio . Aplicando a lei de Gauss para essa superfície, temos:
A carga dentro da nossa superfície nesse caso é carga da esfera mais a carga da casca condutora, então:
Com isso, ficamos com:
Podemos jogar para fora da integral pelo mesmo motivo de antes, com isso temos que:
Então temos que o campo nessa região é dado por:
Podemos ver que o campo cai com nessa região.
Passo 5
Agora vamos atrás do que é pedido em . Para isso vamos usar que:
Como o campo em todas a regiões é radial, só a parte relacionada a vai nos interessar de .
Então para , temos que:
Integrando os dois lados temos:
Segundo o enunciado temos que ter para , então temos que , assim temos:
Passo 6
Agora vamos avaliar a região onde . Fazendo o mesmo que fizemos antes, temos:
Integrando os dois lados, temos:
Usando a condição de contorno de que em o potencial da região onde deve ser igual ao potencial da região , assim:
Com isso temos que:
Passo 7
Agora vamos para a região , nessa região temos o campo elétrico igual a zero, então nosso potencial acaba sendo zero nessa região.
Por último vamos analisar a região onde .
Vamos fazer a mesma coisa que fizemos anteriormente, assim temos que:
Integrando os dois lados, temos que:
Pelas condições de contorno temos que o potencial em na região , deve ser igual ao potencial em na região , já que não tem porque o valor do potencial ser descontinuo tirando o condutor, então:
Assim temos que:
Passo 8
Agora vamos atrás do trabalho pedido em , temos que encontrar aqui o trabalho realizado pelo campo elétrico, isso é, pela força elétrica. Lembrando que, como a força elétrica é uma força conservativa, o seu trabalho é dado por:
Isso é, o trabalho será igual a menos a variação de energia potencial elétrica, e a energia potencial elétrica é:
Aqui, queremos o trabalho realizado para ir do ponto até o ponto , logo:
Onde, temos que:
Jogando isso na equação para o trabalho, temos:
Com isso temos que:
Prontinho, conseguimos fazer tudo que o problema pedia!
Resposta
:
:
:
:
:
:
:
: