Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Momento de Inércia

Ver Teoria
Exercício 111234567891012131415161718

Enunciado

19) Uma lâmina tem a forma de um hemisfério de raio de raio a . Calcule o momento de inércia dessa lâmina em relação a um eixo que passa pelo polo e é perpendicular ao plano que delimita o hemisfério. Considere a densidade no ponto P da lâmina proporcional à distância desse ponto ao plano que delimita o hemisfério.

Passo 1

Antes de entender a matemática da coisa vamos entender a geografia da coisa kkkk. Porque, cara, pensa comigo, o que é um hemisfério lá em geografia? É a metade da terra, certo?

Aqui não será diferente! O hemisfério que a gente quer, pode ser esse de cima aí, o Norte.

O problema quer o momento de inércia em relação a algum eixo que passa pelo polo! Sim! O Polo Norte nesse caso. Se imaginarmos a Terra agora como uma semiesfera de raio a e ao redor do eixo z , o eixo que passa pelo polo é justamente o eixo z ...

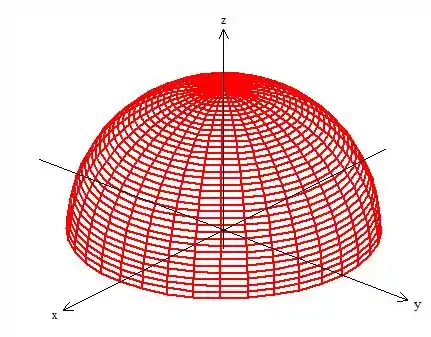
Pegou a montagem da coisa? Então agora vamos à matemática!

Passo 2

Traduzindo o enunciado da geografia para a matemática: queremos o momento de inércia da semiesfera de raio a em relação ao eixo z , dado por...

I z = ∬ S   x 2 + y 2 ρ x ,   y ,   z d S

Onde ρ x ,   y ,   z é a função de densidade da semiesfera. O problema também fala algo a respeito dessa função de densidade:

“Considere a densidade no ponto P da lâmina proporcional à distância desse ponto ao plano que delimita o hemisfério”

Ora, o plano que delimita o hemisfério é o plano z = 0 e a distância de qualquer ponto em relação a esse plano é dado pela “alturinha” z do ponto.

ρ x ,   y ,   z = k z

k é a constante de proporcionalidade.

Então o momento de inércia que queremos calcular no final de contas é...

I z = k ∬ S   x 2 + y 2 z d S

Bora?

Passo 3

Para resolver uma integral de superfície escalar como essa, vamos realizar basicamente três procedimentos centrais:

1º - Parametrizar a superfície S .

2º - Encontrar o termo d S .

3º - Substituir os termos da parametrização na função a ser integrada.

Passo 4

Já sabemos quem é a superfície S que queremos o momento de inércia:

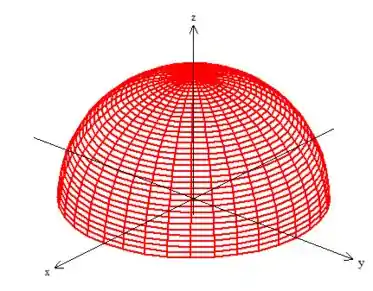
Semiesferas podem ser parametrizadas com as primas das coordenadas esféricas...

x = ρ sin ⁡ φ cos ⁡ θ

y = ρ sin ⁡ φ sin ⁡ θ

z = ρ cos ⁡ θ

A diferença é que agora o ρ é o raio da esfera que é fixo – não muda. Ou seja, ρ = a ...

x = a sin ⁡ φ cos ⁡ θ

y = a sin ⁡ φ sin ⁡ θ

z = a cos ⁡ θ

Lembre-se de que a é o raio da semiesfera que o problema pediu para considerar. Ele é um número e não um parâmetro. Sabendo disso a parametrização da esfera ficou então...

σ φ ,   θ = a sin ⁡ φ cos ⁡ θ ,   a sin ⁡ φ sin ⁡ θ ,   a cos ⁡ θ

Passo 5

É importante conhecermos o domínio dos parâmetros... Onde eles variam, saca?

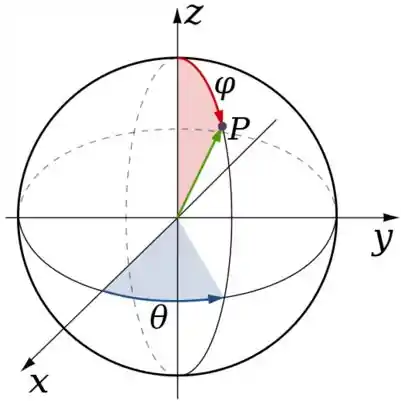
O θ gira uma volta completa para fazer a semiesfera...

0 ≤ θ ≤ 2 π

Já o φ , varia entre...

0 ° ≤ φ ≤ 90 ° →

0 ≤ φ ≤ π 2

Passo 6

Falta-nos encontrar o termo d S ... Bem, poderíamos encontra fazendo o modelo clássico:

d S = N →   d θ d φ

Onde...

N → = ∂ σ θ ,   φ ∂ θ × ∂ σ θ ,   φ ∂ φ

Mas cara, não disse que a parametrização é prima das coordenadas esféricas? Então, ela se parece até nisso com ela. Ora quem é o Jacobiano lá?

J = ρ 2 sin ⁡ φ

Então, o módulo do vetor normal será quase isso, basta trocar o ρ pelo raio da esfera...

N → = a 2 sin ⁡ φ

Então...

d S = a 2 sin ⁡ φ   d θ d φ

Passo 7

Antes de retornar à integral

I z = k ∬ S   x 2 + y 2 z d S

e simplesmente substituirmos tudo, vamos transformar a função escalar que estamos integrando em termos dos parâmetros da superfície...

x 2 + y 2 z     →

Como sabemos...

x = a sin ⁡ φ cos ⁡ θ

y = a sin ⁡ φ sin ⁡ θ

z = a cos ⁡ φ

Então...

x 2 + y 2 z     →         a 2 sin 2 ⁡ φ cos 2 ⁡ θ + a 2 sin 2 ⁡ φ sin 2 ⁡ θ a cos ⁡ φ   →

a 2 sin 2 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ a cos ⁡ φ   →

a 2 sin 2 ⁡ φ ⋅ a cos ⁡ φ   →

a 3 sin 2 ⁡ φ cos ⁡ φ

Passo 8

Dado as variações dos parâmetros...

0 ≤ θ ≤ 2 π

0 ≤ φ ≤ π 2

E lembrando que...

d S = a 2 sin ⁡ φ   d θ d φ

e acabamos de ver...

x 2 + y 2 z     →   a 3 sin 2 ⁡ φ cos ⁡ φ

A integral de superfície então se transforma em uma...

I z = k ∬ S   x 2 + y 2 z   d S =

k ∫ 0 2 π ∫ 0 π 2 a 3 sin 2 ⁡ φ cos ⁡ φ ⋅ a 2 sin ⁡ φ   d φ d θ =

Como a é constante...

I z = k a 5 ∫ 0 2 π ∫ 0 π 2 sin 3 ⁡ φ cos ⁡ φ   d φ d θ

Integral Dupla. ! Bora calcula-la?

Passo 9

I z = k a 5 ∫ 0 2 π ∫ 0 π 2 sin 3 ⁡ φ cos ⁡ φ   d φ d θ = k a 5 ∫ 0 2 π ∫ 0 π 2 sin 3 ⁡ φ cos ⁡ φ   d φ d θ =

Fazendo uma substituição...

t = sin ⁡ φ       →           d t = cos ⁡ φ

Mas não se esquecendo de trocar também os limites...

φ = 0               →                   t = sin ⁡ 0 = 0

φ = π 2               →                   t = sin ⁡ π 2 = 1

Ganhamos...

k a 5 ∫ 0 2 π ∫ 0 π 2 sin 3 ⁡ φ cos ⁡ φ   d φ d θ = k a 5 ∫ 0 2 π ∫ 0 1 t 3 d t d θ =

k a 5 ∫ 0 2 π t 4 4 0 1 d θ = k a 5 4 ∫ 0 2 π d θ =

k a 5 4 2 π =

k a 5 2

Resposta

k π a 5 2

Exercícios de Livros Relacionados

Dê uma expressão integral para o momento de inércia I z em torno do eixo z de uma folha fina no formato da suerfície S , se a função densidade é ρ .Determine o momento de inércia em torno do eixo z do
Seja S a parte da esfera x 2 + y ² + z ² = 25 ² ² que está acima do plano z = 4 . Se S tiver densidade constante k , encontre ( a ) o centro de massa e ( b ) o momento de inércia em torno do eixo z .
Determine o centro de massa do hemisfério x 2 + y 2 + z 2 = a 2 , z ≥ 0 , se ele tiver densidade constante.
Uma superfície S é representada pela equação vetorial r →u , v= 4 cos ⁡ u ,4 s e nu,4 v 0 ≤ u ≤ 2 π 0 ≤ v ≤ 2 Determinar a equação cartesiana de SDesenhar sobre a superfície S as curvas coordenadas ob
Calcule o momento de inércia da superfície homogênea, de massa M , de equação x 2 + y 2 = R 2( R0 ) , com 0 ≤ z ≤ 1 em torno do eixo O z .