Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Momento de Inércia

Ver Teoria
Exercício 131234567891011121415161718

Enunciado

Integrais de superfície – caso escalar

Determine a massa da superfície z 2 = 3 x 2 + 3 y 2 que satisfaz z ≥ 0 e x 2 + y 2 ≤ 2 y , com densidade δ x , y , z = x 2 + y 2 .

Passo 1

Para acharmos a massa, temos que fazer a integral de superfície da densidade, ou seja, vai ser uma parada assim

M = ∬ S δ x , y , z d S

Antes de tudo, vamos pensar que superfície é essa do problema. Temos um cone elíptico, cortado pelo plano z = 0 e pelo cilindro x 2 + y 2 = 2 y .

Nossa superfície é, portanto, essa aqui:

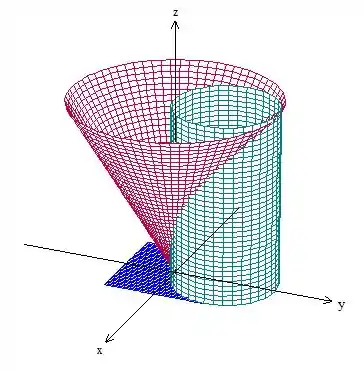
S é a parte do cone acima do plano azul e dentro do cilindro:

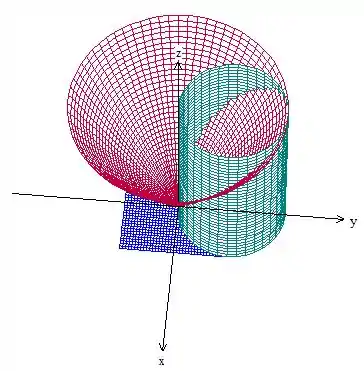
Passo 2

Agora vamos parametrizar essa superfíce em coordenadas cilíndricas, ok? Temos:

x = r cos ⁡ θ

y = r   s e n   θ

z = z

Aplicando no cone:

z 2 = 3 x 2 + 3 y 2

z 2 = 3 r 2

z = 3 r

O que nos dá

φ r , θ = ( r cos ⁡ θ ,   r   s e n   θ , 3 r )

Agora vamos descobrir os intervalos. Sabemos que o raio vai desde r = 0 até a equação do cilindro, fazendo a mudança cilíndrica nele:

x 2 + y 2 = 2 y

r 2 = 2   r   s e n   θ

r = 2   s e n   θ

Logo, 0 ≤ r ≤ 2   s e n   θ .

Como temos meia volta em torno do eixo z , 0 ≤ θ ≤ π .

Passo 3

Agora temos que calcular a normal ∂ φ ∂ r × ∂ φ ∂ θ

Temos:

∂ φ ∂ r = cos ⁡ θ , s e n   θ , 3

∂ φ ∂ θ = ( - r   s e n   θ , r cos ⁡ θ , 0 )

∂ φ ∂ r × ∂ φ ∂ θ = i ^ j ^ k ^ cos ⁡ θ s e n   θ 3 - r   s e n   θ r cos ⁡ θ 0 = - 3 r cos ⁡ θ , - 3 r   s e n   θ , r cos 2 ⁡ θ + r   s e n 2 θ

= - 3 r cos ⁡ θ , - 3 r   s e n   θ , r

Passo 4

Tirando o módulo desse vetor:

∂ φ ∂ r × ∂ φ ∂ θ = - 3 r cos ⁡ θ 2 + - 3 r   s e n   θ 2 + r 2

= 3 r 2 + r 2 =

= 2 r

Passo 5

Agora, para calcular essa integral, vamos usar a seguinte fórmula:

M = ∬ S δ x , y , z d S = ∬ D δ φ r , θ N r , θ d r d θ

Escrevendo a função nas variáveis da parametrização:

δ x , y , z = x 2 + y 2

δ φ r , θ = r 2 cos 2 ⁡ θ + r 2 s e n 2 θ = r

Levando para a integral:

M = ∬ D r .   2 r   d r d θ

Trazendo os intervalos de D :

= 2 ∫ 0 π ∫ 0 2   s e n   θ r 2 d r d θ =

Passo 6

Agora vamos resolver isso aí

= 2 ∫ 0 π r 3 3 0 2   s e n   θ d θ =

= 2 3 ∫ 0 π 8   s e n 3 θ d θ =

= 16 3 ∫ 0 π   s e n 3 θ d θ =

= 16 3 ∫ 0 π   s e n   θ ( 1 - cos 2 ⁡ θ ) d θ =

Fazendo

cos ⁡ θ = u

- s e n   θ   d θ = d u

θ = 0           →           u = 1

θ = π         →           u = - 1

= - 16 3 ∫ 1 - 1 ( 1 - u 2 ) d u =

= - 16 3 u - u 3 3 1 - 1 =

= - 16 3 - 1 + 1 3 - 1 + 1 3 =

= 64 9

Resposta

64 9

Exercícios de Livros Relacionados

Dê uma expressão integral para o momento de inércia I z em torno do eixo z de uma folha fina no formato da suerfície S , se a função densidade é ρ .Determine o momento de inércia em torno do eixo z do
Seja S a parte da esfera x 2 + y ² + z ² = 25 ² ² que está acima do plano z = 4 . Se S tiver densidade constante k , encontre ( a ) o centro de massa e ( b ) o momento de inércia em torno do eixo z .
Determine o centro de massa do hemisfério x 2 + y 2 + z 2 = a 2 , z ≥ 0 , se ele tiver densidade constante.
Uma superfície S é representada pela equação vetorial r →u , v= 4 cos ⁡ u ,4 s e nu,4 v 0 ≤ u ≤ 2 π 0 ≤ v ≤ 2 Determinar a equação cartesiana de SDesenhar sobre a superfície S as curvas coordenadas ob
Calcule o momento de inércia da superfície homogênea, de massa M , de equação x 2 + y 2 = R 2( R0 ) , com 0 ≤ z ≤ 1 em torno do eixo O z .