Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Momento de Inércia

Ver Teoria
Exercício 171234567891011121314151618

Enunciado

Mostre que o momento de inércia de uma casca cilíndrica de comprimento L e raio da base a , com densidade constante, em relação a um diâmetro do círculo cujo centro coincide com o centro da casca cilíndrica, é I = 1 2 M a 2 + 1 12 M L 2 , onde M é a massa total.

Passo 1

Calma! Esse enunciado é bem confuso, tem muita informação e não deixa nada claro o que precisamos fazer e como precisamos.

Na primeira parte do enunciado, ele vai descrever a nossa superfície. Ele diz que é uma “casca cilíndrica de comprimento L e raio a ”, vamos escrevê-la centrada na origem para facilitar as futuras contas. Assim:

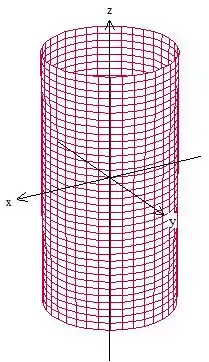
Em seguida, ele diz que o eixo que o momento de inercia deve ser calculado é “um diâmetro do círculo cujo centro coincide com o centro da casca cilíndrica”. Confuso né? Vamos por parte, o centro da casca cilíndrica se encontra exatamente na metade da altura do cilindro, por isso centralizamos o cilindro na origem! O circulo que possui a origem como centro é esse aqui

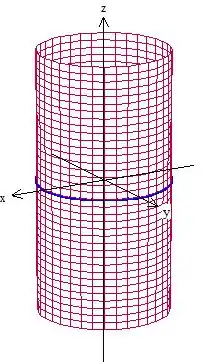
Portanto, o eixo que vamos calcular o momento de inércia é qualquer diâmetro dessa circunferência! Podemos escolher por exemplo o eixo x . O momento de inércia é dado por

I x = ∬ S ( y 2 + z 2 ) δ ( x , y , z ) d S

Na próxima parte tem uma informação importante, o enunciado diz que a nossa densidade é constante, só que ele não diz o seu valor! Só diz mais pra frente que M é a massa total, como vamos fazer pra encontrar a densidade? Precisamos dela para fazer o cálculo do momento de inércia.

Existe uma solução não muito trivial, a definição de densidade no caso de uma placa é

δ = M Á r e a

A massa M é um dos parâmetros dado, a área do cilindro é fácil de calcular, ela é dada pela fórmula

Á r e a = 2 π r . H

No nosso caso, o raio r = a e a altura H = L , portanto a densidade é dada por

δ = M 2 π a L

Tendo esclarecido isso, podemos seguir para o passo a passo de momento de inércia.

Passo 2

Vamos parametrizar a superfície primeiro, temos um cilindro, então é justo fazer a parametrização em coordenadas cilíndricas. O raio do cilindro é igual a a , portanto

x = a cos ⁡ t

y = a sen ⁡ t

z = z

Os limites de integração da superfície são

- L 2 ≤ z ≤ L 2

0 ≤ t ≤ 2 π

Esses limites de z porque centralizamos o cilindro, lembra? Pode existir outra parametrização, escolhemos essa aqui.

Passo 3

Tendo isso, vamos agora encontrar o vetor normal. Precisamos das derivas em relação às duas variáveis

∂ φ ∂ t = - a sen ⁡ t , a cos ⁡ t , 0

∂ φ ∂ z = 0,0 , 1

N → = i j k - a sen ⁡ t a cos ⁡ t 0 0 0 1

= ( a cos ⁡ t , a sen ⁡ t ,   0 )

N → = a 2 cos 2 ⁡ t + a 2 sen 2 ⁡ t = a 2 = a

Passo 4

-

Vamos substituir tudo na integral agora

I x = ∬ S y 2 + z 2 δ x , y , z d S

Como a densidade e o modulo da normal N → são constantes, vamos colocar seus valores para fora da integral já

= M 2 π a L . a ∫ 0 2 π ∫ - L 2 L 2 a 2 sen 2 ⁡ t + z 2 d z d t =

= M 2 π L ∫ 0 2 π a 2 sen 2 ⁡ t z + z 3 3 z = - L 2 z = L 2

= M 2 π L ∫ 0 2 π a 2 sen 2 ⁡ t L 2 - - L 2 + L 3 8 - - L 3 8 3 d t =

= M 2 π L ∫ 0 2 π L a 2 sen 2 ⁡ t + L 3 12 d t =

Vamos cortar o L do denominador com os de dentro da integral, fica assim

= M 2 π ∫ 0 2 π a 2 sen 2 ⁡ t + L 2 12 d t

Para integrarmos aqui, vamos usar essa equação aqui

sen 2 ⁡ t = 1 - cos ⁡ 2 t 2

Além disso, vamos dividir as integrais em duas pra facilitar nas contas

M a 2 2 π ∫ 0 2 π 1 - cos ⁡ 2 t 2 d t + M L 2 2 π ∫ 0 2 π 1 12 d t =

= M a 2 2 π t 2 - sen ⁡ 2 t 4 t = 0 t = 2 π + M L 2 2 π t 12 t = 0 t = 2 π =

Aqui o seno vai zerar, então o restante fica

= M a 2 2 π 2 π 2 + M L 2 2 π 2 π 12 =

= M a 2 2 + M L 2 12

Pronto, exatamente o que o enunciado fala, demonstramos o que ele pediu! :D

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Dê uma expressão integral para o momento de inércia I z em torno do eixo z de uma folha fina no formato da suerfície S , se a função densidade é ρ .Determine o momento de inércia em torno do eixo z do
Seja S a parte da esfera x 2 + y ² + z ² = 25 ² ² que está acima do plano z = 4 . Se S tiver densidade constante k , encontre ( a ) o centro de massa e ( b ) o momento de inércia em torno do eixo z .
Determine o centro de massa do hemisfério x 2 + y 2 + z 2 = a 2 , z ≥ 0 , se ele tiver densidade constante.
Uma superfície S é representada pela equação vetorial r →u , v= 4 cos ⁡ u ,4 s e nu,4 v 0 ≤ u ≤ 2 π 0 ≤ v ≤ 2 Determinar a equação cartesiana de SDesenhar sobre a superfície S as curvas coordenadas ob
Calcule o momento de inércia da superfície homogênea, de massa M , de equação x 2 + y 2 = R 2( R0 ) , com 0 ≤ z ≤ 1 em torno do eixo O z .