Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Momento de Inércia

Ver Teoria
Exercício 123456789101112131415161718

Enunciado

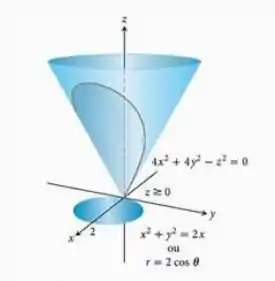
Encontre o momento de inércia em relação ao eixo z de uma casca fina de densidade constante δ cortada do cone 4 x 2 + 4 y 2 - z 2 = 0 ,   z ≥ 0 , pelo cilindro circular x 2 + y 2 = 2 x

Passo 1

Para encontrar o momento de inércia devemos calcular:

I z = ∬ D ( x 2 + y 2 ) δ d S

Para resolver esta integral devemos saber o módulo do vetor normal à superfície e para isto vamos parametrizar ela.

Podemos usar a parametrização:

x = r s e n θ y = r c o s θ z = 2 r

Assim a superfície é parametrizada por,

φ r ,   θ = ( r s e n θ ,   r c o s θ ,   2 r )

Passo 2

Encontrando o módulo do vetor normal,

N → r ,   θ = ∂ φ ∂ r × ∂ φ ∂ θ

N → ( r ,   θ ) =   i j k s e n θ c o s θ 2 r c o s θ r s e n θ 0

N → r ,   θ = ( 2 r s e n θ ,   2 r c o s θ ,   - r )

N → r ,   θ = 4 r 2 s e n 2 θ + 4 r 2 cos 2 ⁡ θ + r 2

Usando a relação fundamental da trigonometria s e n 2 θ + cos 2 ⁡ θ = 1 ,  

N → r ,   θ = 5 r 2 = r 5

Passo 3

Agora vamos resolver a integral de superfície,

I z = ∬ D ( x 2 + y 2 ) δ d S

Como δ é constante:

I z = δ ∬ S ( r 2 s e n 2 θ + r 2 cos 2 ⁡ θ ) r 5 d r d θ

I z = δ 5 ∬ S r 3 d r d θ

Queremos a parte da cônica que se encontra dentro do cilindro r = 2 s e n θ

I z = δ 5 ∫ - π / 2 π / 2 ∫ 0 2 c o s θ r 3 d r d θ

I z = δ 5 ∫ - π / 2 π / 2 ∫ 0 2 c o s θ r 3 d r d θ

I z = δ 5 ∫ - π / 2 π / 2 r 4 4 0 2 c o s θ d θ = δ 5 ∫ - π / 2 π / 2 1 4 16 cos 4 ⁡ θ d θ = 4 δ 5 ∫ - π / 2 π / 2 cos 4 ⁡ θ d θ  

Esta integral é difícil de resolver, vamos resolver ela no próximo passo e depois voltamos para terminar o exercício!

Passo 4

Para resolver esta integral, vamos utilizar a seguinte igualdade trigométrica:

c o s 2 θ = 2 cos 2 ⁡ θ - 1 → cos 2 ⁡ θ = cos ⁡ 2 θ + 1 2  

Assim, temos que:

cos 4 ⁡ θ = cos ⁡ 2 θ + 1 2 4   = cos 2 ⁡ 2 θ + 2 cos ⁡ 2 θ + 1 4

Integrando,

∫ - π / 2 π / 2 c o s 4 θ d θ = 1 4 ∫ - π / 2 π / 2 ( cos 2 ⁡ 2 θ + 2 cos ⁡ 2 θ + 1 ) d θ

Mas,

cos 2 ⁡ 2 θ = cos ⁡ 4 θ + 1 2

Substituindo,

∫ - π / 2 π / 2 c o s 4 θ d θ = 1 4 ∫ - π / 2 π / 2 cos ⁡ 4 θ + 1 2 + 2 cos ⁡ 2 θ + 1 d θ

∫ - π / 2 π / 2 c o s 4 θ d θ = 1 4 ∫ - π / 2 π / 2 cos ⁡ 4 θ + 4 cos ⁡ 2 θ + 3 2 d θ

Como,

∫ cos ⁡ n θ d θ = sen ⁡ n θ n + C

∫ - π 2 π 2 c o s 4 θ d θ = 1 8 sen ⁡ 4 θ 4 + 4 sen ⁡ 2 θ 2 + 3 θ - π 2 π 2 = 3 π 8

Passo 5

Voltando ao nosso problema, temos:

I z =   4 δ 5 ∫ - π / 2 π / 2 cos 4 ⁡ θ d θ

Substituindo o resultado encontrado,

I z =   4 δ 5 ⋅ 3 π 8 = 3 π δ 5 2

Resposta

I z = 3 π δ 5 2

Exercícios de Livros Relacionados

Dê uma expressão integral para o momento de inércia I z em torno do eixo z de uma folha fina no formato da suerfície S , se a função densidade é ρ .Determine o momento de inércia em torno do eixo z do
Seja S a parte da esfera x 2 + y ² + z ² = 25 ² ² que está acima do plano z = 4 . Se S tiver densidade constante k , encontre ( a ) o centro de massa e ( b ) o momento de inércia em torno do eixo z .
Determine o centro de massa do hemisfério x 2 + y 2 + z 2 = a 2 , z ≥ 0 , se ele tiver densidade constante.
Uma superfície S é representada pela equação vetorial r →u , v= 4 cos ⁡ u ,4 s e nu,4 v 0 ≤ u ≤ 2 π 0 ≤ v ≤ 2 Determinar a equação cartesiana de SDesenhar sobre a superfície S as curvas coordenadas ob
Calcule o momento de inércia da superfície homogênea, de massa M , de equação x 2 + y 2 = R 2( R0 ) , com 0 ≤ z ≤ 1 em torno do eixo O z .