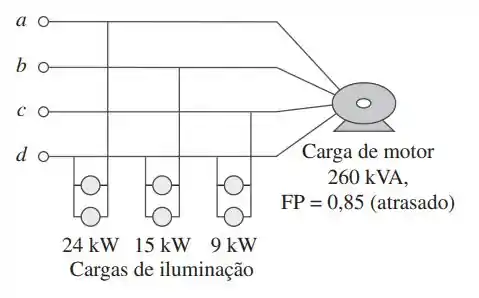
Conforme indicado na figura, uma linha trifásica quadrifilar com tensão de fase igual a e sequência de fase positiva alimenta uma carga de motor equilibrada acom . A carga do motor está conectada a três linhas principais indicadas por e. Além disso, lâmpadas incandescentes (FP unitário) são ligadas como segue: da linha para o neutro, da linha para o neutro e da linha para o neutro.
(a) se forem dispostos três wattímetros para medir a potência em cada linha, calcule a leitura de cada medidor.
(b) determine a magnitude da corrente na linha do neutro.
Passo 1
Calma lá que essa questão é gigante e parece difícil por causa desse estranho aí, mas na real é bem tranquila!
Vamos começar calculando a potência ativa do motor já que ele só nos deu a potência aparente (em kVA):
Agora com isso, podemos achar a potência por fase que precisamos para poder achar a potência total de cada fase (que é exatamente o que o wattímetro vai ler, e daí já matamos a primeira questão).
Então, cada wattímetro vai ler:
Passo 2
Para a corrente de neutro, o motor não contribui com corrente de neutro pois é equilibrado. Então vamos calcular cada corrente utilizando a Primeira Lei de Ohm:
Vamos calcular as correntes com seus respectivos ângulos (sequência de fase positiva)
Passo 3
Agora, a corrente de neutro será a soma de tudo, então, pra isso, vamos passar tudo para a forma retangular:
Resposta
(a)
(b)