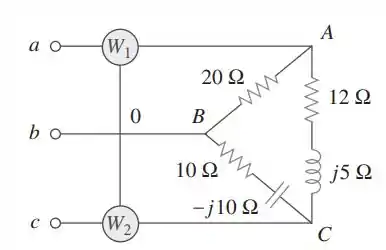
Na figura, dois wattímetros estão conectados apropriadamente à carga desequilibrada alimentada por uma fonte equilibrada tal que com sequência de fases positiva.
(a) Determine a leitura de cada wattímetro.
(b) Calcule a potência aparente total absorvida pela carga.
Passo 1
Vamos separar as tensões na sequência de fases positiva:
Daí, vamos calcular as correntes de cada fase pra poder depois calcular a potência de cada fase e consequentemente as leituras de cada wattímetro.
Vamos calcular agora cada corrente de linha (das fases A e B que é o que o enunciado pede):
Fase A:
Fase C:
Calculando as potências:
Mas, como , então,
Passo 2
Agora, para a potência total, basta somar tudo e depois achar cada potência (ativa, reativa e, então, aparente)
Resposta
(a)
(b)
Exercícios de Livros Relacionados
Para o circuito mostrado na Figura P11.20, determinea) as correntes de fase I A B ,I B CeI C A ,b) as correntes de linha I a A ,I b BeI c C , quando Z 1=2,4-j 0,7 Ω ;Z 2=8+j 6Ω ;eZ 3=20 +j 0Ω .: