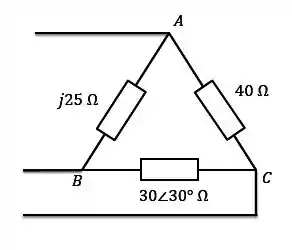
Uma fonte trifásica com tensão de linha e sequência de fase positiva tem uma carga conectada em triângulo desequilibrada, conforme indicado na figura abaixo. Determine as correntes de fase e a potência complexa total.
Passo 1
Primeiro, vamos determinar as tensões. Como foi dito que a sequência de fase é positiva e foi dado o valor do módulo da tensão de linha:
Passo 2
Para calcular as correntes de fase, vamos utilizar a Lei de Ohm:
Passo 3
A potência complexa em cada fase será:
Passo 4
Agora que calculamos a potência complexa em cada uma das fases, para calcularmos a potência complexa total, temos que somar cada parcela:
Resposta
Exercícios de Livros Relacionados
Para o circuito mostrado na Figura P11.20, determinea) as correntes de fase I A B ,I B CeI C A ,b) as correntes de linha I a A ,I b BeI c C , quando Z 1=2,4-j 0,7 Ω ;Z 2=8+j 6Ω ;eZ 3=20 +j 0Ω .: