Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos Trifásicos Desequilibrados

Ver Teoria
Exercício 31245678910

Enunciado

Determine as correntes de linha para o circuito trifásico abaixo:

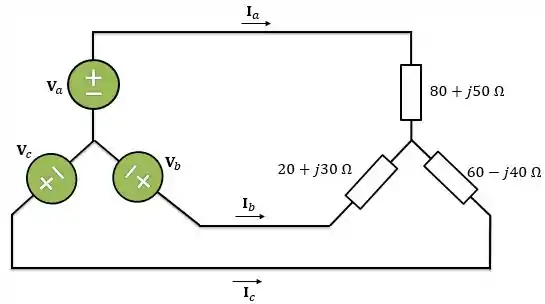
Seja

V a = 110 ∠ 0 ° ,                 V b = 110 ∠ - 120 ° ,     V c = 110 ∠ 120 °   V

Passo 1

Para esse circuito vamos utilizar análise de malhas para determinar as correntes de linha. Para isso, vamos escolher os sentidos para as correntes de malha I 1 e I 2 :

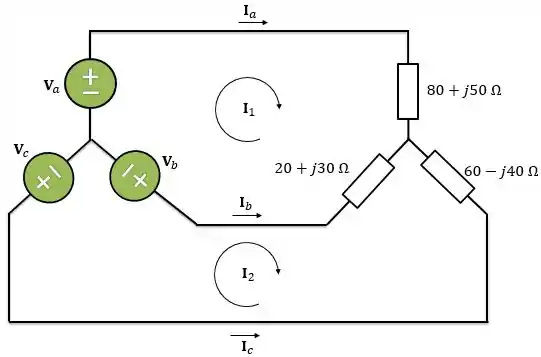
Passo 2

Aplicando a lei das tensões de Kirchhoff na malha 1 , temos:

110 ∠ - 120 ° - 110 ∠ 0 ° + 80 + j 50 I 1 + 20 + j 30 I 1 - I 2 = 0

100 + j 80 I 1 - 20 + j 30 I 2 = 110 ∠ 0 ° - 110 ∠ - 120 °

100 + j 80 I 1 - 20 + j 30 I 2 = 110 - ( - 55 - j 95,26 )

100 + j 80 I 1 - 20 + j 30 I 2 = 110 + 55 + j 95,26

100 + j 80 I 1 - 20 + j 30 I 2 = 165 + j 95,26       ( i )

Passo 3

Aplicando a lei das tensões de Kirchhoff na malha 2 , temos:

110 ∠ 120 ° - 110 ∠ - 120 ° + 20 + j 30 I 2 - I 1 + 60 - j 40 I 2 = 0

- 20 + j 30 I 1 + 80 - j 10 I 2 = 110 ∠ - 120 ° - 110 ∠ 120 °

- 20 + j 30 I 1 + 80 - j 10 I 2 = - 55 - j 95,26 - ( - 55 + j 95,26 )

Chegamos na equação final:

- 20 + j 30 I 1 + 80 - j 10 I 2 = - j 190,52       ( i i )

Passo 4

Temos duas equações e duas incógnitas. Primeiro, vamos isolar I 1 na primeira equação:

I 1 = 165 + j 95,26 + 20 + j 30 I 2 100 + j 80

I 1 = 190,52 ∠ 30 ° 128,06 ∠ 38,66 ° + 36,05 ∠ 56,31 ° 128,06 ∠ 38,66 ° I 2

I 1 = 1,488 ∠ - 8,66 ° + ( 0,281 ∠ 17,65 ° ) I 2

Agora, vamos substituir na equação final encontrada no passo 3:

- 20 + j 30 ( 1,488 ∠ - 8,66 ° + 0,281 ∠ 17,65 ° I 2 ) + 80 - j 10 I 2 = - j 190,52

( - 36,05 ∠ - 123,69 ° ) ( 1,488 ∠ - 8,66 ° + 0,281 ∠ 17,65 ° I 2 ) + 80 - j 10 I 2 = - j 190,52

- 53,65 ∠ - 132,35 ° + 10,13 ∠ - 106,04 ° I 2 + 80 - j 10 I 2 = - j 190,52

- 2,8 - j 9,736 + 80 - j 10 I 2 = - j 190,52 + 36,14 + j 39,65

I 2 = 36,14 - j 150,87 77,2 - j 19,736

I 2 = 155,14 ∠ - 76,52 ° 79,68 ∠ - 14,34 °

I 2 = 1,947 ∠ - 62,18 °   A

Passo 5

Substituindo o valor que encontramos para I 2 na equação abaixo, temos:

I 1 = 1,488 ∠ - 8,66 ° + ( 0,281 ∠ 17,65 ° ) I 2

I 1 = 1,488 ∠ - 8,66 ° + ( 0,281 ∠ 17,65 ° ) ( 1,947 ∠ - 62,18 ° )

I 1 = 1,488 ∠ - 8,66 ° + 0,547 ∠ - 44,53 °

I 1 = 1,471 - j 0,224 + 0,390 - j 0,384

I 1 = 1,861 - j 0,608   A

I 1 = 1,958 ∠ - 18,09 °   A

Passo 6

Analisando o circuito, temos que:

I a = I 1

I b = I 2 - I 1

I c = - I 2

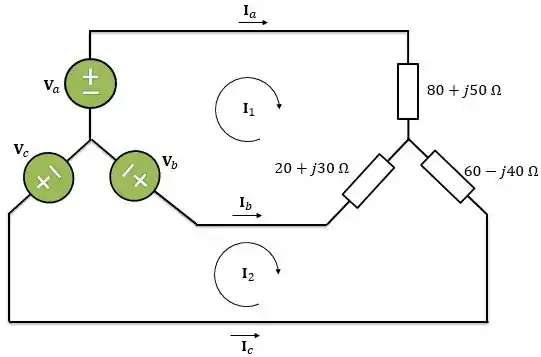
Portanto, as correntes de linha serão:

I a = 1,958 ∠ - 18,09 °   A

I b = ( 1,947 ∠ - 62,18 °   ) - ( 1,861 - j 0,608 )

I b = ( 0,908 - j 1,722   ) - ( 1,861 - j 0,608 )

I b = - ( 0,952 + j 1,113 )   A

I b = - 1,465 ∠ 49,45 °   A

I b = 1,465 ∠ - 130,55 °   A

I c = - 1,947 ∠ - 62,18 °

I c = 1,947 ∠ 117,82 °   A

Resposta

I a = 1,958 ∠ - 18,09 °   A

I b = 1,465 ∠ - 130,55 °   A

I c = 1,947 ∠ 117,82 °   A

Exercícios de Livros Relacionados

Para o circuito mostrado na Figura P11.20, determinea) as correntes de fase I A B ,I B CeI C A ,b) as correntes de linha I a A ,I b BeI c C , quando Z 1=2,4-j 0,7 Ω ;Z 2=8+j 6Ω ;eZ 3=20 +j 0Ω .: