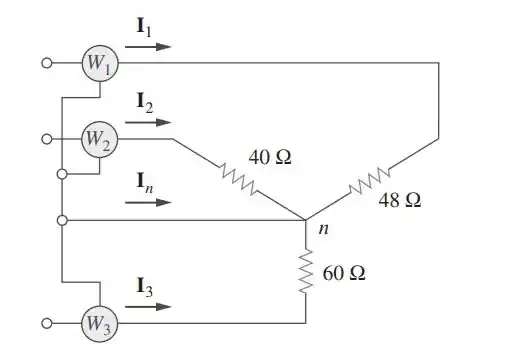
Um sistema trifásico quadrifilar operando com tensão de linha igual a é mostrado na figura. As tensões da fonte estão equilibradas. A potência absorvida pela carga resistiva conectada em estrela é medida pelo método dos três wattímetros. Calcule:
(a) A tensão para o neutro.
(b) As correntes e.
(c) As leituras dos wattímetros.
(d) A potência total absorvida pela carga
Passo 1
Na letra (a) ele quer apenas a tensão de fase que é a tensão para o neutro. Como o enunciado nos dá a tensão de linha, então:
Passo 2
Na letra (b) vamos começar assumindo que a sequência é positiva pois não foi dito nada no enunciado sobre a sequência de fase.
Vamos calcular cada corrente separadamente pois é um sistema desequilibrado por causa das diferentes resistências na carga.:
Para a corrente de neutro vamos fazer uma análise nodal e passar todas as correntes para sua forma retangular para facilitar nossa soma:
ou
Passo 3
Agora na letra C, queremos as leituras dos Wattímetros que nada mais é do que calcular as potências em cada fase:
Passo 4
Para a potência total, basta somar todas as potências calculadas no passo 3:
Resposta
(a)
(b)
(c)
(d)